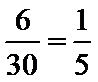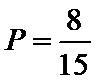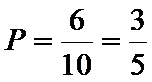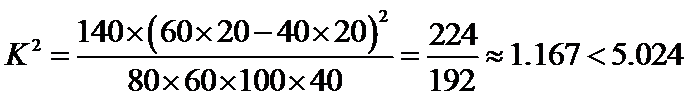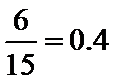- 实际推断原理和假设检验的应用
- 共4题
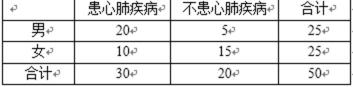
18. 近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院的50人进行了问卷调查得到了如下的列联表:
(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,再从6人中选2人,求恰有一名女性的概率?
(Ⅱ)为了研究心肺疾病是否与性别有关,请计算出统计量K2,你有多大的把握认为心肺疾病与性别有关?
下面的临界值表供参考:
正确答案
(1)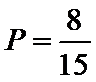
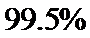
解析
试题分析:本题属于考查了分层抽样和古典概型以及独立性检验,(1)先利用分层抽样的方法计算出男女各抽多少人,然后利用古典概型公式计算;(2)利用独立性检验的方法来解(Ⅰ)解:在患心肺疾病人群中抽6人,则抽取比例为
∴ 女性应该抽取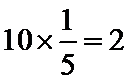
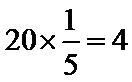
女性2人记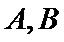
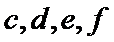
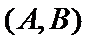
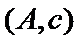
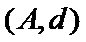
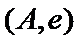

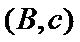
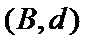
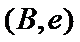
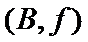
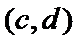
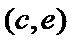
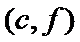
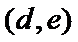
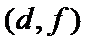
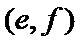
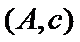
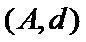
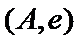
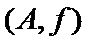
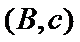
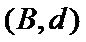
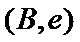
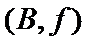
故上述抽取的6人中选2人,恰有一名女性的概率概率为
(Ⅱ):∵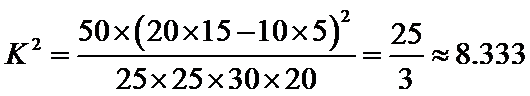
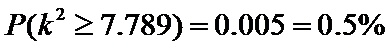
那么,我们有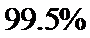
考查方向
解题思路
本题考查古典概型和独立性检验,解题步骤如下:(1)先利用分层抽样的方法计算出男女各抽多少人,然后利用古典概型公式计算;(2)利用独立性检验的方法来解。
易错点
分类容易遗漏。
知识点
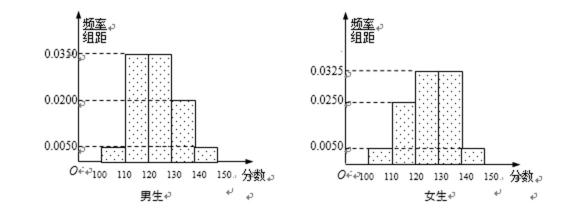
18.某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,
附:
正确答案
(1)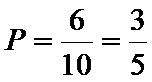
解析
试题分析:本题属古典概型及独立性检验,(1)先根据分层抽样算出抽出的人数,然后利用古典概型的公式计算;(2)列出联表然后代入公式计算出k的观测值,然后下结论。
试题解析:(1)解:由已知得,抽取的100名学生中,男生60名,女生40名
分数小于等于110分的学生中,
男生人有60×0.05 = 3(人),记为A1,A2,A3;女生有40×0.05 = 2
从中随机抽取2名学生,所有的可能结果共有10种,
(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)
其中,两名学生恰好为一男一女的可能结果共有6种,它们是:(A1,B1),(A1,B2),
(A2,B1),(A2,B2),(A3,B1),(A3,B2),
故所求的概率
(2)解:由频率分布直方图可知,
在抽取的100名学生中,男生 60×0
据此可得2×2列联表如下:
所以得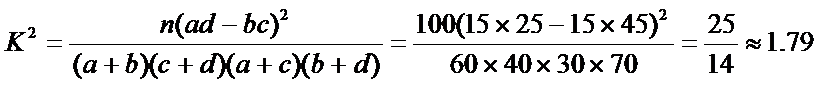
因为1.79 < 2.706.
所以没有90%的把握认为“数学尖子生与性别有关”.
考查方向
解题思路
本题考查了古典概型及独立性检验,解题步骤如下:(1)先根据分层抽样算出抽出的人数,然后利用古典概型的公式计算;(2)列出联表然后代入公式计算出k的观测值,然后下结论。
易错点
在找基本事件的个数的时候有可能遗漏或者重复。
知识点
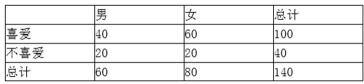
周立波是海派清口创始人和《壹周·立波秀》节目的主持人,他的点评视角独特,语言幽默犀利,给观众留下了深刻的印象.某机构为了了解观众对《壹周·立波秀》节目的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
20,根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关.(精确到0.001)
21.从19题中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱《壹周·立波秀》节目的概率.
正确答案
喜爱的观众有4名;不喜爱的观众有2名.
解析
抽样比为

考查方向
解题思路
直接计算抽样比,即可算出喜爱与不喜爱的人数;
易错点
对“独立性检验的思想”不理解易出错
正确答案
不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
解析
假设:观众性别与喜爱无关,由已知数据可求得,
∴ 不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
考查方向
解题思路
直接代入公式计算
易错点
对“独立性检验的思想”不理解易出错
正确答案
0.4
解析
记喜爱的4名男性观众为a,b,c,d,不喜爱的2名男性观众为1
其中选到的两名观众都喜爱的事件有6个,
故其概率为
考查方向
解题思路
直接列出总事件及发生事件的情况,直接求比。
易错点
对“独立性检验的思想”不理解易出错
周立波是海派清口创始人和《壹周·立波秀》节目的主持人,他的点评视角独特,语言幽默犀利,给观众留下了深刻的印象.某机构为了了解观众对《壹周·立波秀》节目的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
20,根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关.(精确到0.001)
21.从19题中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱《壹周·立波秀》节目的概率.
正确答案
喜爱的观众有4名;不喜爱的观众有2名.
解析
抽样比为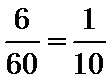
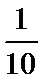
考查方向
解题思路
直接计算抽样比,即可算出喜爱与不喜爱的人数;
易错点
对“独立性检验的思想”不理解易出错
正确答案
不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
解析
假设:观众性别与喜爱无关,由已知数据可求得,
∴ 不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
考查方向
解题思路
直接代入公式计算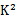
易错点
对“独立性检验的思想”不理解易出错
正确答案
0.4
解析
记喜爱的4名男性观众为a,b,c,d,不喜爱的2名男性观众为1
其中选到的两名观众都喜爱的事件有6个,
故其概率为
考查方向
解题思路
直接列出总事件及发生事件的情况,直接求比。
易错点
对“独立性检验的思想”不理解易出错
扫码查看完整答案与解析