三角函数中的恒等变换应用
共232题

· 三角函数中的恒等变换应用

三角函数中的恒等变换应用
共232题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

在△ABC中，角A、B、C所对的边分别为a、b、c，且满足cos2C－cos2A＝2sin（＋C）·sin（－C）．

17.求角A的值；

18.若a＝且b≥a，求2b－c的取值范围．

第(1)小题正确答案及相关解析

正确答案

见解析

解析

解：（1）由已知得

化简得，故．

考查方向

本题主要考察了二倍角的余弦公式，考察了两角和与差的正弦公式，考察了三角函数的恒等变换及化简求值，考察了余弦定理的应用，均值定理

解题思路

该题解题思路如下

1）利用倍角公式对解析式降次

2）利用特殊角的三角函数求值得到角A，

3）使用正弦定理，进行边角之间的转换

4）根据角的取值范围得到答案

易错点

该题易于忽略了对A的范围的判断，该题属于中档题

第(2)小题正确答案及相关解析

正确答案

见解析

解析

解：

（2）由正弦定理，得，…7分

因为，所以，，

故=

所以．

考查方向

本题主要考察了二倍角的余弦公式，考察了两角和与差的正弦公式，考察了三角函数的恒等变换及化简求值，考察了余弦定理的应用，均值定理

解题思路

该题解题思路如下

1）利用倍角公式对解析式降次

2）利用特殊角的三角函数求值得到角A，

3）使用正弦定理，进行边角之间的转换

4）根据角的取值范围得到答案

易错点

该题易于忽略了对A的范围的判断，该题属于中档题

题型：单选题

单选题 · 5 分

5.知函数，，则下列结论中正确的是（）

A函数的最小正周期为

B函数的最大值为2

C将函数的图象向左平移单位后得的图象

D将函数的图象向右平移单位后得的图象

正确答案

解析

将2个函数利用诱导公式先进行化简，，所以=，故A,B都错，所以选D答案。

考查方向

函数的图像与性质。

解题思路

逐一进行判断。

易错点

性质弄错。

知识点

三角函数中的恒等变换应用

题型：填空题

填空题 · 6 分

11.函数的最小正周期是，最小值是．

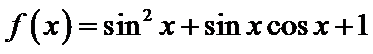
正确答案

，；

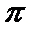
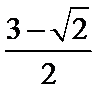
解析

试题分析：利用二倍角公式，两角差的正弦公式转化为一个角的三角函数，然后求出最小正周期和最小值。

∵＝，

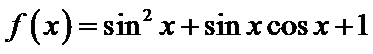
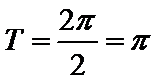
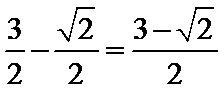
∴最小正周期，最小值为：．

故答案为：，.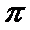

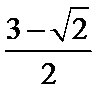
考查方向

本题主要考察了三角函数恒等变换的应用和最值、正弦函数的图像和性象，本题属于基础题．

解题思路

由三角函数恒等变换化简解析式可得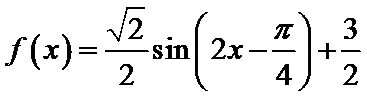，由正弦函数的图象和性质即可求得最小正周期，最小值．

易错点

三角函数中三角公式的灵活应用.

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

10．若函数（）的最小正周期为，则在区间上的值域为

正确答案

解析

，，则，当x在上的值域就为，所以选A选项。

考查方向

本题主要考查了简单的三角恒等变换。

解题思路

先用诱导公式化简，在用辅助角公式合二为一，最后可以求出其值域。

易错点

本题不会使用诱导公式已经辅助角公式。

知识点

三角函数中的恒等变换应用

题型：单选题

单选题 · 5 分

8.设实数a，b，t满足|a+1|=|sinb|=t（）

A若t确定，则唯一确定

B若t确定，则唯一确定

C若t确定，则唯一确定

D若t确定，则唯一确定

正确答案

解析

试题分析：根据题中给出的条件确定a，b，t的关系，利用排除法找出答案。

∵实数a，b，t满足|a+1|=t，∴，，

t确定，则为定值．，A，C不正确，

∴若t确定，则唯一确定，

故选B.

考查方向

本题考察了命题的判断真假，本题属于基础题．

解题思路

根据代数式得出，，运用条件，结合三角函数可判断答案．

易错点

利用已知条件找出a，b，t的关系.

知识点

三角函数中的恒等变换应用

继续学习学习下一知识点

下一知识点 : 诱导公式的推导

百度题库 > 高考 > 文科数学 > 三角函数中的恒等变换应用

扫码查看完整答案与解析