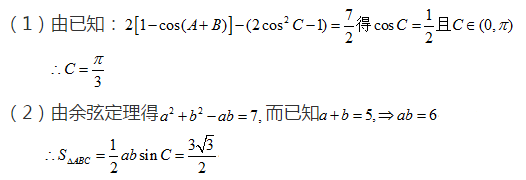- 三角函数中的恒等变换应用
- 共232题
19.设函数f(x)=alnx+
(1)求b;
(2)若存在x0≥1,使得f(x0)<
正确答案
见解析。
解析
(1)f′(x)=
∴f′(1)=a+(1﹣a)×1﹣b=0,解得b=1.
(2)函数f(x)的定义域为(0,+∞),由(1)可知:f(x)=alnx+
∴

①当a

∴函数f(x)在(1,+∞)单调递增,
∴存在x0≥1,使得f(x0)<


解得
②当

则当x∈

当x∈

∴存在x0≥1,使得f(x0)<

而


③若a>1时,f(1)=
综上可得:a的取值范围是
知识点
1. 下列关于不等式的说法正确的是( )
正确答案
解析
根据基本不等式成立的条件是“一正二定三相等”可知A不正确,因为a、b不一定是正实数;C中一元二次方程的根是1+a和1-a,但是当



知识点
直线

正确答案
解析
直线






知识点
已知椭圆C的中点在原点,焦点在x轴上,离心率等于

(1)求椭圆C的方程;
(2)P(2,3),Q(2,-3)是椭圆上两点,A、B是椭圆上位于直线PQ两侧的两动点,若直线AB的斜率为
正确答案
见解析。
解析
(1)设


由
∴椭圆C的方程为
(2)设


代入
由

由韦达定理得
四边形
∴当

知识点
16. 在△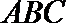

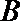
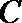
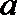
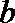
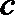
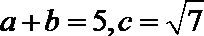
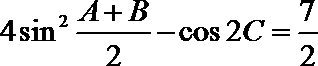
(Ⅰ)求角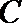
(Ⅱ)求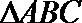
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.对于命题p:

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 在







(Ⅰ)求角
(Ⅱ)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求
(2)将




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析