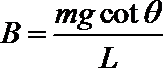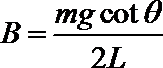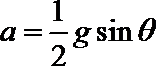- 牛顿第二定律
- 共448题
13.如图,水平地面上的矩形箱子内有一倾角为θ的固定斜面,斜面上放一质量为m的光滑球.静止时,箱子顶部与球接触但无压力.箱子由v开始向右做匀加速运动,当速度达到2v时,立即改做加速度大小为a的匀减速运动直至静止,从加速开始经过的总路程为s.
(1)求箱子加速阶段的加速度大小a′.
(2)若a>gtanθ,求减速阶段球受到箱子左壁和顶部的作用力.
正确答案
解:(1)设加速度为a′,由匀变速直线运动的公式:
得:s=s1+s2
解得:
(2)设小球不受车厢的作用力,应满足:Nsinθ=ma
Ncosθ=mg
解得:a=gtanθ
减速时加速度的方向向左,此加速度有斜面的支持力N与左壁支持力共同提供,当a>gtanθ 时,
左壁的支持力等于0,此时小球的受力如图,
则:Nsinθ=ma
Ncosθ﹣F=mg
解得:F=macotθ﹣mg
解析
解析已在路上飞奔,马上就到!
知识点
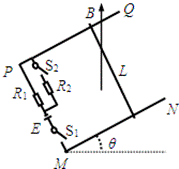
7. 如图所示,两根电阻不计的平行光滑金属导轨PQ、MN与水平面的夹角均为θ,整个装置处于竖直向上的匀强磁场中,导轨下端接有图示电路;已知:电阻R1 =6Ω、R2=3Ω,电源电动势E=6V,内阻不计。当电键S1闭合,S2断开时,一根垂直于导轨PQ放置的电阻不计、质量均匀的金属棒恰好能静止,金属棒质量为m,平行导轨间距为L.则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示,一质量m=0.4kg的小物块,以v0=2m/s的初速度,在与斜面成某一夹角的拉力F作用下,沿斜面向上做匀加速运动,经t=2s的时间物块由A点运动到B点,A、B之间的距离L=10m.已知斜面倾角θ=30°,物块与斜面之间的动摩擦因数μ=
(1)求物块加速度的大小及到达B点时速度的大小.
(2)拉力F与斜面的夹角多大时,拉力F最小?拉力F的最小值是多少?
正确答案
解:(1)物体做匀加速直线运动,根据运动学公式,有:

v=v0+at ②
联立解得;
a=3m/s2
v=8m/s
(2)对物体受力分析,受重力、拉力、支持力和滑动摩擦力,
如图
根据牛顿第二定律,有:
平行斜面方向:Fcosα﹣mgsin30°﹣Ff=ma
垂直斜面方向:Fsinα+FN﹣mgcos30°=0
其中:Ff=μFN
联立解得:
F=
故当α=30°时,
拉力F有最小值,为
解析
解析已在路上飞奔,马上就到!
知识点
1.关于火箭点火升空这一瞬间的火箭的速度和加速度的判断,下列说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.某物体A静止于水平地面上,它与地面间的动摩擦因数μ=0.2,若给物体A一个水平向右的初速度v0=10m/s,g=10m/s2。求:
(1)物体A向右滑行的最大距离?
(2)若物体A右方x0=12m处有一辆汽车B,在物体A获得初速度v0的同时,汽车B从静止开始以a=2m/s2的加速度向右运动,通过计算说明物体A能否撞上汽车B?
正确答案
(1)由牛顿第二定律得
μmg = ma0
a0 = 2 m/s2
根据 v2 – v02 = - 2 a0 x
x = 25m
(2)假设二者不相撞,设经过时间t二者有共同速度v
则对物体A v = v0 –a0t
对汽车B v = at
v = 5 m/s
t = 2.5 s
该过程中物体A的位移 xA = 
该过程中汽车B的位移 xB = 
因为 xA > xB + x0
故物体A能击中汽车B
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析