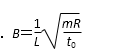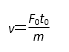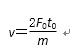- 牛顿第二定律
- 共448题
17.在稳定轨道上的空间站中,物体处于完全失重状态。有如下图所示的装置,半径分别为r和R(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,宇航员让一小球以一定的速度先滑上甲轨道,通过粗糙的CD段,又滑上乙轨道,最后离开两圆轨道,那么下列说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
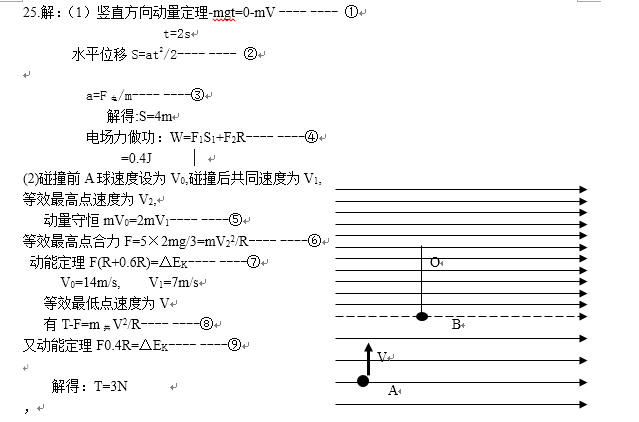
25.如图所示,在竖直边界线




(1)求物块到达C点时的速度大小。
(2)求物块到达D点时所受轨道的压力大小。
(3)物块从D点进入电场的瞬间,将匀强电场的方向变为水平方向,并改变电场强度的大小,使物块恰好能够落到B点,求电场强度的大小和方向(取
正确答案
(1)物块由A点至C点的运动过程中,根据动能定理可得:
解得:
(2)物块在由C点至D点的运动过程中,根据机械能守恒定律可得:

物块运动到最高点时,根据牛顿第二定律可得:
联立解得:vD=4m/s,FN=22N
(3)物块进入电场后,沿水平方向做初速度 的匀变速运动,沿竖直方向做自由落体运动,设其沿水平方向上的加速度为a,物体由 点运动到B点所用的时间为t,则有:
L=
解得:
又由
解得:
解析
解析已在路上飞奔,马上就到!
知识点
22.民用航空客机的机舱,除了有正常的舱门和舷梯连接,供旅客上下飞机外,一般还配有紧急出口.发生意外情况的飞机在着陆后,打开紧急出口的舱门,会自动生成一个气囊(由斜面部分AC和水平部分CD构成),机舱中的人可沿该气囊滑行到地面上来,如下图所示.某机舱离气囊底端的竖直高度AB=3.0 m,气囊构成的斜面长AC=5.0 m,AC与地面之间的夹角为θ. 斜面部分AC和水
正确答案
解析:人的受力如图所示,由牛顿运动定律得mgsin θ-μFN=ma
FN-mgcos θ=0
则a=gsin θ-μgcos θ=1.6 m/s2
设人在斜面部分滑下所用的时间为t1,
s=at,t1=2.5 s
设人滑到斜面底端C时的速度为vC,
vC=at1=4 m/s
由牛顿运动定律得μmg=ma′
由0-vC=(-a′)t2
解得t2=0.73 s)
故人从开始到滑到E点所用的时间t=t1+t2=3.23 s.
解析
解析已在路上飞奔,马上就到!
知识点
22.如图所示,水平桌面上有一小车,装有砂的砂桶通过细绳给小车施加一水平拉力,小车从静止开始做直线运动。保持小车的质量M不变,第一次实验中小车在质量为m1的砂和砂桶带动下由静止前进了一段距离s;第二次实验中小车在质量为m2的砂和砂桶带动下由静止前进了相同的距离s,其中m1<m2<M。两次实验中,绳对小车的拉力分别为T1 和T2,小车、砂和砂桶系统的机械能变化量分别为ΔE1和ΔE2,若空气阻力和摩擦阻力的大小保持不变,不计绳、滑轮的质量,则下列分析正确的是( )
A.(m1g-T1)<(m2g-T2),ΔE1=ΔE2
B.(m1g-T1)=(m2g-T2),ΔE1=ΔE2
C.(m1g-T1)<(m2g-T2),ΔE1<ΔE2
D.(m1g-T1)=(m2g-T2),ΔE1<ΔE2
正确答案
A
解析
设空气阻力和摩擦阻力的合力为







知识点
4.如图所示,竖直平面内有一固定的光滑绝缘椭圆大环,水平长轴为AC,竖直短轴为ED。轻弹簧一端固定在大环的中心O,另一端连接一个可视为质点的带正电的小环,小环刚好套在大环上,整个装置处在一个水平向里的匀强磁场中。将小环从A点由静止释放,已知小环在A、D两点时弹簧的形变量大小相等。下列说法中错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.19世纪匈牙利物理学家厄缶就明确指出:“沿水平地面向东运动的物体,其重量(即:列车的视重或列车对水平轨道的压力)一定要减轻。”后来,人们常把这类物理现象称为“厄缶效应”。如图所示:我们设想,在地球赤道附近的地平线上,有一列质量是M的列车,正在以速率v,沿水平轨道匀速向东行驶。已知:(1)地球的半径R;(2)地球的自转周期T。今天我们像厄缶一样,如果仅考虑地球自转的影响(火车随地球做线速度为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
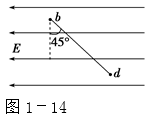
11.如图1-14所示,一带电液滴在重力和匀强电场对它的作用力作用下,从静止开始由b沿直线运动到d,且bd与竖直方向所夹的锐角为45°,则下列结论正确的是( )
正确答案
解析
每小题给出的四个选项中,有的小题只有一个选项符合题目要求,有些小题有多个选项符合题目要求,全部选对的得5分,选不全的得2分,有选错或不答的得0分
知识点
26.如图所示,三个质量均为
































(1)滑块





(3)弹簧最初的弹性势能
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.如图,虚线下方有足够大的场强大小E=5.0×103 V/m和上方场强为8mg/3q的匀强电场,方向均水平向右。质量均为m=1.5×10-2kg的A、B小球,其中B球为绝缘小球且不带电,被长为R的绝缘丝线悬挂在O点刚好静止在虚线上, A球带电荷量为qA=+6.0×10-6C,在竖直平面内的以某一初速度v竖直进入电场,运动到B点速度刚好水平,同时与B球发生正碰并立即粘在一起围绕O点做半径为R=0.7m完整的圆周运动,假设甲、乙两球可视为质点,g取10 m/s2。(sin53°=0.8,c0s53°=0.6)
(1)假设初速度v=20m/s ,试求小球A与B球碰撞前能运动的水平位移的大小和整个过程中电场力对小球做功的最大值。
(2)如果小球刚好能做完整的圆周运动,试求碰撞前A球的最小速度和绳子所受的最大拉力分别多大。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图甲所示,MN左侧有一垂直纸面向里的匀强磁场。现将一边长为L、质量为m、电阻为R的正方形金属线框置于该磁场中,使线框平面与磁场方向垂直,且bc边与磁场边界MN重合。当t=0时,对线框施加一水平拉力F,使线框由静止开始向右做匀加速直线运动;当t=t0时,线框的ad边与磁场边界MN重合。图乙为拉力F随时间t变化的图线。由以上条件可知,磁场的磁感应强度B的大小及t0时刻线框的速率v为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析