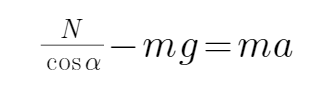- 牛顿第二定律
- 共448题
已定义ch为字符型变量,以下赋值语句中错误的是
A.ch='\';
B.ch=62+3;
C.ch=NULL;
D.ch='\xaa';
正确答案
A
解析
暂无解析
如图所示,在竖直平面内有一光滑的
14.A运动到圆弧轨道最低点时的速率
15.A运动到圆弧轨道最低点时对圆弧轨道的压力
16.A和B碰撞过程中系统损失的机械能
正确答案
v1 =4m/s
解析
A从圆弧轨道最高点运动到最低点过程中:mgR =

解得:v1 =4m/s ··········································································2分
考查方向
动能定理
解题思路
A从圆弧轨道最高点运动到最低点过程中,根据动能定理列式求解速度。
易错点
简单题不应该出错
正确答案
FN´= 30N
解析
A在圆弧轨道最低点时:
FN-mg=m
解得:FN = 30 N ··········································································1分
根据牛顿第三定律,小球对轨道的压力大小FN´= 30N···················1分
考查方向
向心力、牛顿第二定律
解题思路
A在圆弧轨道最低点时,根据合外力提供向心力结合牛顿第三定律求解小球对轨道的压力。
易错点
基础题不应该出错
正确答案
ΔE=4J
解析
A和B碰撞过程中:mv1=2mv ··························································2分
ΔE=


解得:ΔE=4J ················································································2分
考查方向
动量守恒定律
解题思路
A和B碰撞过程中系统动量守恒,根据动量守恒定律以及能量守恒定律列式求解即可.
易错点
注意使用动量守恒定律时要规定正方向
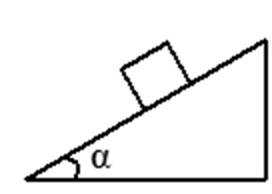
6.质量为m的小物块放在倾角为α的斜面上处于静止,如图所示.若整个装置可以沿水平方向或竖直方向平行移动, 且小物块与斜面体总保持相对静止.下列的哪种运动方式可以使物块对斜面的压力和摩擦力都一定减少( )
正确答案
解析
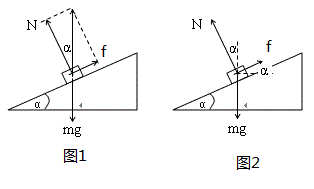
A、设向上的加速度大小为a.物块受到重力mg、斜面的支持力N和摩擦力f三个力作用,物块的加速度方向竖直向上,根据牛顿第二定律可知物体所受的合外力方向竖直向上,而重力竖直向下,则知N和f的合力方向必定竖直向上,如图1所示,
根据牛顿第二定律得
解得,N=m(g+a)cosα,f=m(g+a)sinα
物块原来处于静止状态,a=0,N=mgcosα,f=mgsinα
可见,物块沿竖直方向向上加速运动时,所受的支持力和摩擦力都增大,则物块对斜面的压力和摩擦力都一定增大.故A错误.
B、与A同理可得,物块沿竖直方向向上减速运动时,所受的支持力和摩擦力都减小,则物块对斜面的压力和摩擦力都一定减小.故B正确.
C、物块沿水平方向向右加速运动时,受力如图2所示,根据牛顿第二定律得:
fcosα-Nsinα=ma
fsinα-Ncosα=0
解得,N=mgcosθ-masinθ,f=mgsinθ+macosθ
可见,N减小,f增大,故C错误.
D、与C同理可知,物块沿水平方向向右减速运动时,当加速度a增大时,N增大,而f可能减小,也可能先减小到零后反向增大.故D错误.
故选B
考查方向
共点力平衡的条件及其应用.
解题思路
分析物体的受力情况,根据牛顿第二定律列式,分析物块所受的斜面的支持力和静摩擦力的变化,即可得解.
易错点
析受力情况,根据牛顿第二定律得到两个力的表达式,再进行分析,是常用的方法.
知识点
2.如图所示是男子体操项目中的“单臂大回环”。运动员单手抓住单杠,伸展身体,从静止开始以单杠为轴做圆周运动。已知运动员质量为60kg,若忽略运动过程中空气阻力及手与单杠间摩擦,则运动员到达最低点时手臂所受拉力约为()
正确答案
解析
设人的长度为L人的重心在人体的中间.最高点的速度最小为零,根据动能定理得:
解得最低点人的速度为
根据牛顿第二定律得:
解得:F=5mg=5×600=3000N.故C正确.
故选:C.
考查方向
动能定理、向心力
解题思路
人在最高点的最小速度为零,根据动能定理求出人在最低点的速度,再根据牛顿第二定律求出拉力的大小.
易错点
关键知道最高点的最小速度为零.
知识点
如图所示,一轻弹簧一端与竖直墙壁相连,另一端与放在光滑水平面上的长木板左端接触,轻弹簧处于原长,长木板的质量为M,一物块以初速度






29.滑块上长木板的一瞬间,长木板的加速度大小;
30.长木板向左运动的最大速度;
31.长木板的长度
正确答案
解析
物块滑上长木板时,长木板受到的合外力等于滑块对长木板的摩擦力,由牛顿第二定律得:μmg=Ma
解得,长木板的加速度
考查方向
牛顿第二定律
解题思路
物块在长木板滑动时,长木板受到的合外力等于滑块对长木板的摩擦力,由牛顿第二定律求出长木板的加速度.
易错点
滑块上长木板的一瞬间,弹簧还没有被压缩,此时长木板受到的合力为滑块对长木板的摩擦力.
正确答案
解析
当长木板向左运动的最大速度时,弹簧的弹力等于滑块对长木板的摩擦力,即 kx=μmg,解得
长木板从开始运动到速度最大的过程,设最大速度为v,由动能定理得:
解得:
考查方向
动能定理;牛顿运动定律的综合应用
解题思路
当长木板向左运动的最大速度时,弹簧的弹力等于滑块对长木板的摩擦力,由胡克定律求弹簧的压缩量.长木板从开始运动到速度最大的过程,运用动能定理求最大速度.
易错点
关键分析清楚长木板的运动情况,当长木板的加速度为0时,长木板速度最大.
正确答案
解析
当弹簧的压缩量达到最大时,木板的速度为零,木块的速度也为零,设长木板的长度为L,根据能量守恒定律得:
解得:
考查方向
功能关系
解题思路
当弹簧的压缩量达到最大时,木板的速度为零,木块的速度也为零,根据能量守恒定律求长木板的长度.
易错点
抓住弹簧的压缩量达到最大时,木板和木块的速度均为零,运用能量守恒定律列式求解.
扫码查看完整答案与解析