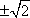向量的减法及其几何意义
共14题

· 向量的减法及其几何意义

向量的减法及其几何意义
共14题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

在△ABC中，M是BC的中点，AM＝3，BC＝10，则__________。

正确答案

－16

解析

·＝(＋)·(＋)＝＋·＋·＋·＝||2＋(＋)·＋||||cosπ＝9－25＝－16

知识点

向量的减法及其几何意义

题型：简答题

简答题 · 12 分

如图，四棱锥中，,，侧面为等边三角形，，.

（1）证明：；

（2）求与平面所成角的大小。

正确答案

见解析。

解析

【解析1】

（1）取中点，连接，则四边形为矩形，，连接，则，。

又，故，所以为直角。

由，，，得，所以。

与两条相交直线、都垂直，所以。

（2）由知，，作，垂足为，则，。

作，垂足为，则，连接，则。

又，，故，。

作，为垂足，则。，即到平面的距离为。

由于，所以，到平面的距离。

设与平面所成的角为，则，。

【解析2】

以为坐标原点，射线为轴的正半轴，建立如图所示的空间坐标系。

设，则，，又设，则，，。

（1）,,,由得

解得，由得，又由得，即，故，。

于是，，，，，，故，，又，所以。

（2）设平面的法向量，则，，，，又，，故

取得，又，。

故与平面所成得角为。

【解析3】

（1）计算，，，于是，利用勾股定理，可知，同理，可证，又，因此。

（2）过点D做，如图建立空间直角坐标系。

，，，，可计算平面的一个法向量是，，。

知识点

向量的减法及其几何意义

题型：填空题

填空题 · 4 分

设R)。记为平行四边形ABCD内部（不含边界）的整点的个数，其中整点是指横、纵坐标都是整数的点，则；的所有可能取值为。

正确答案

6；6,7,8

解析

在, , 时分别对应点为，在平面直角坐标系中画出平行四边形，其中位于原点，位于正半轴；设与边的交点为，

与边的交点为，四边形内部（不包括边界）的整点都在线段上，线段上的整点有3个或4个，所以，不难求得点，

①当为型整数时，都是整点，

②当为型整数时，，都不是整点，

③当为型整数时，，都不是整点，（以上表述中为整数）上面3种

情形涵盖了的所有整数取值，所以的值域为.

知识点

向量的减法及其几何意义

题型：单选题

单选题 · 5 分

若直线不平行于平面，且，则

A内存在直线与异面

B内不存在与平行的直线

C内存在唯一的直线与平行

D内的直线与都相交

正确答案

解析

略

知识点

向量的减法及其几何意义

题型：简答题

简答题 · 13 分

设椭圆(a＞b＞0)的左焦点为F，离心率为，过点F且与x轴垂直的直线被椭圆截得的线段长为.

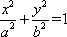
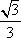
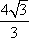
(1)求椭圆的方程；

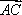
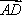
(2)设A，B分别为椭圆的左、右顶点，过点F且斜率为k的直线与椭圆交于C，D两点，若·＋·＝8，求k的值。

正确答案

（1）

（2）k＝

解析

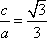
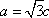
(1)设F(－c,0)，由，知.

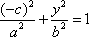
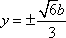
过点F且与x轴垂直的直线为x＝－c，代入椭圆方程有，解得，

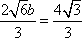
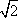
于是，解得b＝，

又a2－c2＝b2，从而a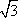＝，c＝1，

所以椭圆的方程为.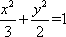

(2)设点C(x1，y1)，D(x2，y2)，由F(－1,0)得直线CD的方程为y＝k(x＋1)，

由方程组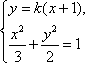消去y，整理得(2＋3k2)x2＋6k2x＋3k2－6＝0.

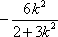
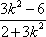
求解可得x1＋x2＝，x1x2＝.

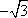
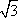
因为A(，0)，B(，0)，

所以·＋·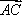

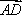
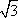
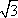
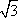
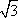
＝(x1＋，y1)·(－x2，－y2)＋(x2＋，y2)·(－x1，－y1)

＝6－2x1x2－2y1y2

＝6－2x1x2－2k2(x1＋1)(x2＋1)

＝6－(2＋2k2)x1x2－2k2(x1＋x2)－2k2

＝.

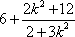
由已知得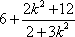＝8，

解得k＝.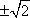

知识点

向量的减法及其几何意义

继续学习学习下一知识点

下一知识点 : 向量的三角形法则

百度题库 > 高考 > 文科数学 > 向量的减法及其几何意义

扫码查看完整答案与解析