- 基本不等式及不等式的应用
- 共144题
20.围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),
其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
正确答案
(Ⅰ)如图,设矩形的另一边长为a m,
则
由已知xa=360,得a=
(II)


即当x=24m时,修建围墙的总费用最小,最小总费用是10440元。
解析
解析已在路上飞奔,马上就到!
知识点
已知f(x)=xlnx,g(x)=-x2+ax-3.
(1)求函数f(x)的单调区间;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明:对一切x∈(0,+∞),都有lnx>
正确答案
见解析
解析
解析:(1)f′(x)=lnx+1,
当x∈时,f′(x)<0,f(x)单调递减;当x∈时,
f′(x)>0,f(x)单调递增。
(2)2xlnx≥-x2+ax-3,则a≤2lnx+x+,
设h(x)=2lnx+x+(x>0),则h′(x)=,
①当x∈(0,1)时,h′(x)<0,h(x)单调递减,
②当x∈(1,+∞)时,h′(x)>0,h(x)单调递增,
所以h(x)min=h(1)=4,对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
所以a≤h(x)min=4.
(3)证明:问题等价于证明xlnx>
由(1)可知f(x)=xlnx(x∈(0,+∞))的最小值是





知识点
若点G为△ABC的重心,且AG⊥BG,则sinC的最大值为 。
正确答案
解析
设AB中点为O,连接AO,可得重心G在CO上且
以AB所在直线为x轴,AB中点为原点建立如图所示直角坐标系
设AB=2,则A(﹣1,0),B(1,0),
设C(x,y),可得G(

∵AG⊥BG,∴点G在以AB为直径的圆上运动(A、B两点除外)
由此可得(

因此,点C在以原点为圆心,半径为3的圆上运动(x轴上两点除外)
在点C的运动中观察∠C的变化,可得当C点在y轴时,∠C达到最大值
而且sinC同时达到最大值。
此时tan


故选:
知识点
某企业有两个生产车间分别在A、B两个位置,A车间有100名员工,B车间有400名员工,现要在公路AC上找一点D,修一条公路BD,并在D处建一个食堂,使得所有员工均在此食堂用餐,已知A、B、C中任意两点间的距离均是1km,设∠BDC=α,所有员工从车间到食堂步行的总路程为S。
(1)写出S关于α的函数表达式,并指出α的取值范围;
(2)问食堂D建在距离A多远时,可使总路程S最少?
正确答案
见解析。
解析
(1)在△BCD中,∵
∴

则


(2)
令S'=0,得
当
当
∴当
此时,


知识点
一直两个非零向量





正确答案
解析
略
知识点
某学校拟建一块周长为400米的操场,如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,矩形的长应该设计成 米。
正确答案
答案:100
解析
略
知识点
若两个正实数



正确答案
解析







知识点
15. 已知函数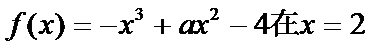

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知点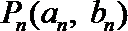


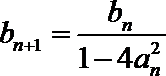

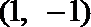
(1)求经过点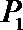

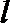
(2)已知点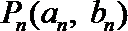





(3)在(2)的条件下,求对于所有


正确答案
(1)
(2)
(3)由(2)得
解析
解析已在路上飞奔,马上就到!
知识点
14.己知平行四边形的周长为6,则其对角线长的平方和的最小值是 .
正确答案
9
解析
试题分析:本题属于平面向量和基本不等式的问题,题目的难度较小。注意转化为平面向量求解。
考查方向
本题主要考查了平面向量和基本不等式的问题。
解题思路
本题考查平面向量,解题步骤如下:
设平行四边形的两邻边分别为向量a,b,夹角为θ。则对角线的平方和为
(a+b)2+(a-b)2=2a2+2b2≥(a+b)2=9。
易错点
本题必须注意转化为平面向量的问题求解,忽视则会出现错误。
知识点
扫码查看完整答案与解析