- 子集与真子集
- 共35题
1
题型:
单选题
|
已知集合A={x|x
正确答案
B
解析
A=(-1,2),故B
知识点
子集与真子集
1
题型:填空题
|
设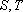
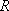
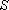
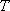
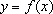
(i)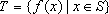
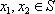
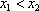
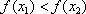
那么称这两个集合“保序同构”,现给出以下3对集合:
①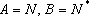
②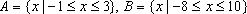
③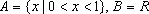
其中,“保序同构”的集合对的序号是()(写出所有“保序同构”的集合对的序号)
正确答案
①②③
解析
本题考查的函数的性质,由题意可知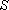
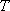
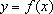
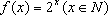
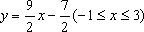
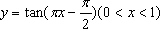
知识点
子集与真子集命题的真假判断与应用
1
题型:简答题
|
设集合



①




(1)求
(2)求

正确答案
(1)4;(2)
解析
(1)当


∴ 
( 2 )任取偶数






由条件知,若



于是



设



当



∴
知识点
元素与集合关系的判断子集与真子集函数解析式的求解及常用方法
1
题型:
单选题
|
若集合

正确答案
C
解析
本题考查的是集合的交集和子集,因为

知识点
子集与真子集交集及其运算
1
题型:
单选题
|
设集合

正确答案
D
解析
略
知识点
子集与真子集交集及其运算
下一知识点 : 集合的相等
扫码查看完整答案与解析








