- 子集与真子集
- 共35题
1.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设A={(x,y)|x2+(y-1)2=1},B={(x,y)|x+y+m≥0},则使A⊆B成立的实数m的取值范围是 。
正确答案
解析
集合A是圆x2+(y-1)2=1上的点的集合,集合B是不等式x+y+m≥0表示的平面区域内的点的集合,要使A⊆B,则应使圆被平面区域所包含(如图)
即直线x+y+m=0应与圆相切或相离(在圆的下方),当直线与圆相切时,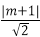
知识点
1.设A,B是全集I={1,2,3,4}的子集,A={l,2},则满足A
正确答案
解析
由A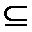
考查方向
解题思路
将几何B按照含有两个元素、三个元素、四个元素的顺利一一列举出来即可。
易错点
在求集合B时忘记{1,2,}导致误选C。
知识点
1.集合
正确答案
解析
由题可得:A中有3个元素,子集有23个。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
直接计算,即可得到结果。
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断端点时发生错误。
知识点
命题“

正确答案
解析
略
知识点
已知函数


(1)若A∪B=B,求实数a的取值范围;
(2)若D⊆C,求实数m的取值范围。
正确答案
见解析。
解析
(1)因为f(x)在[
∵f(

所以,A=[﹣2 1],
又由关于x的不等式

所以,B=(﹣∞,﹣
又A∪B=B,∴A⊆B。
所以,﹣
(2)因为 

对于集合D={x|m+1≤x<2m﹣1}(m>0),若D⊆C,有:
①当 m+1≥2m﹣1时,即 0<m≤2时,D=∅,满足 D⊆C,
②当 m+1<2m﹣1 时,即 m>2时,D≠∅,所以有:
综上:由①②可得:实m的取值范围为(0,3]。
知识点
17.设


正确答案
解:1:当



2:当


综上所述,实数m的取值范围是:
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合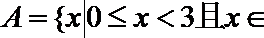
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设集合A={(x,y)|y≥|x-l|},B={(x,y)|x-2y+2≥0),C={(x,y)|ax-y+a≥0},若(A

正确答案
解析
试题分析:本题属于线性规划中的基本问题,题目的难度是逐渐由易到难。注意动直线经过定点.
考查方向
本题主要考查了集合的基本运算和线性规划问题,在近几年的各省高考题出现的频率较高,常与不等式、函数、线性规划等知识点交汇命题。
解题思路
本题考查集合的基本运算和线性规划问题,解题步骤如下:
由题可知,画出A,B集合中的不等式所表示的阴影区域,C集合中的动直线经过定点(-1,0),利用图像易得斜率a≥1。
易错点
本题易在解不等式时发生错误。
知识点
扫码查看完整答案与解析













