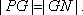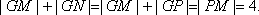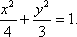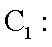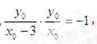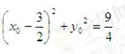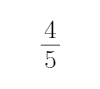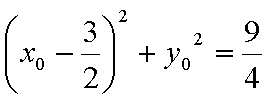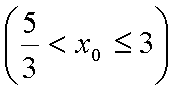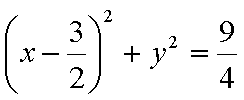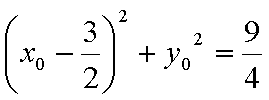- 与圆有关的轨迹问题
- 共1题
已知圆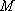
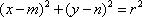
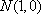
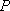
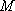
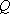
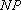
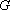
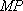
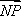
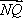

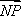

(1)若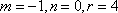
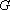
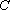
(2)若动圆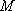
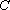
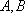
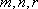
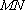
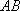
正确答案
见解析。
解析
(1)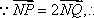
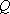
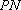
又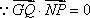
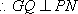
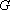
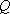
又
∴点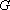
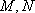
且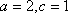
∴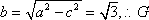
(2)不存在这样一组正实数,下面证明:
由题意,若存在这样的一组正实数,当直线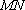
设之为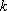

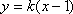
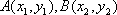
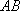
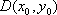
则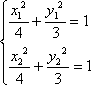
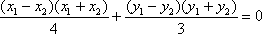
注意到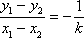
且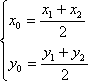
则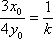
又点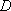
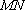
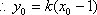
代入②式得: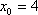
因为弦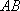
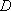
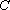
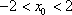
这与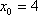
当直线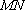
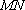
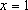
则此时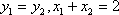
代入①式得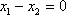
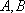
综上,所求的这组正实数不存在。
知识点
20.已知过原点的动直线
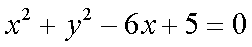
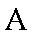
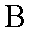
(1)求圆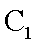
(2)求线段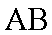
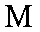

(3)是否存在实数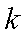
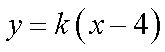

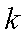
正确答案
(1)圆C1:X2+Y2-6X+5=0化为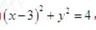
(2)设线段AB的终点M(x0,y0),由圆的性质可得C1M垂直于直线L
设直线L的方程为y=mx,所以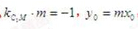
所以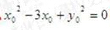
因为动直线L与圆C1相交,所以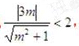
所以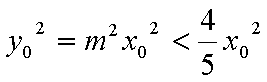
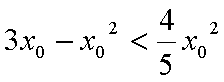
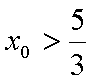
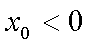
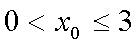
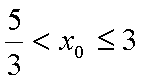
所以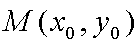
即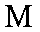

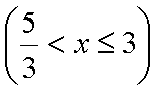
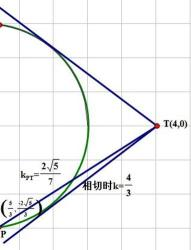
(3)由题意知直线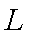
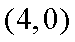
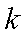
结合图形,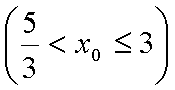
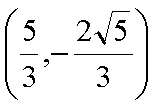
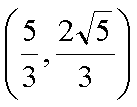
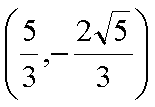
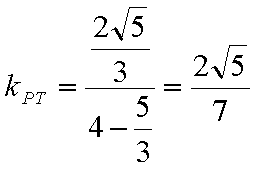
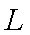

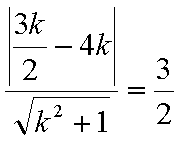
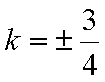
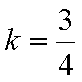
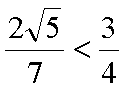
结合图形,可得对于X轴对称下方的圆弧,当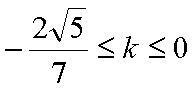
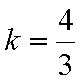
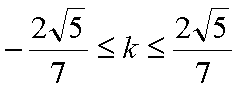
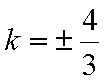
综上所述:当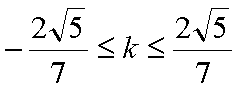
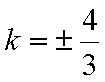
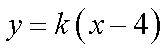

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析