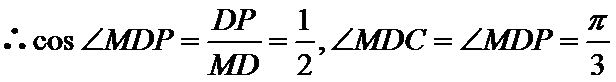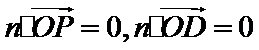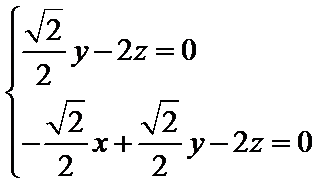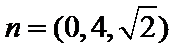直线、平面平行的判定与性质
共531题

直线、平面平行的判定与性质
共531题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

19.如图，已知 DE⊥平面 ACD , DE / / AB ， △ ACD 是正三角形， AD = DE AB=2 ，且 F 是 CD 的中点．

（1）求证：AF //平面 BCE ；

（2）求证：平面 BCE ⊥平面 CDE .

（3）求的值.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质平面与平面垂直的判定与性质

题型：简答题

简答题 · 12 分

17．如图，为圆的直径，点在圆上，，矩形所在的平面和圆所在的平面互相垂直，且。

（1）求证：;

（2）设的中点为，求证：;

（3）设平面将几何体分成的两个椎体的体积分别为。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质

题型：简答题

简答题 · 14 分

17.已知菱形ABCD中，AB=4，（如图1所示），将菱形ABCD沿对角线翻折，使点翻折到点的位置（如图2所示），点E，F，M分别是AB，DC1，BC1的中点．

（Ⅰ）证明：BD //平面；

（Ⅱ）证明：；

（Ⅲ）当时，求线段AC1 的长．

正确答案

证明：（Ⅰ）因为点分别是的中点，

所以．

又平面，平面,

所以平面．

（Ⅱ）

在菱形中，设为的交点,

则．

所以在三棱锥中，

又

所以平面．

又平面，

所以．

（Ⅲ）

连结．在菱形中，，

所以是等边三角形.

所以．

因为为中点，所以．

又，．

所以平面，即平面．

又平面，

所以．

因为，，

所以．

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：简答题

简答题 · 12 分

18．已知四棱锥P—ABCD的底面ABCD是菱形；PA⊥平面ABCD，PA＝AD＝AC，点F为PC的中点．

（1）求证：PA∥平面BFD；

（2）求二面角C—BF—D的正切值的大小．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：简答题

简答题 · 14 分

19.如图，四棱锥中，底面为矩形，平面，为的中点．

（I）证明：平面；

（II）设，，三棱锥的体积，求到平面的距离．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与平面垂直的判定与性质

题型：填空题

填空题 · 5 分

15.设和为不重合的两个平面，给出下列命题：

①若内的两条相交直线分别平行于内的两条直线，则∥；

②若外的一条直线与内的一条直线平行，则∥；

③设，若内有一条直线垂直于，则；

④直线的充要条件是与内的两条直线垂直.

其中所有的真命题的序号是__________ .

正确答案

①②

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用直线与平面平行的判定与性质平面与平面平行的判定与性质直线与平面垂直的判定与性质平面与平面垂直的判定与性质

题型：简答题

简答题 · 14 分

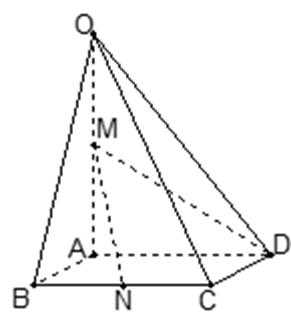
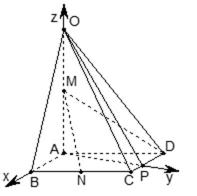
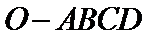
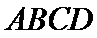
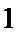
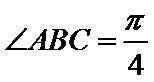
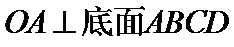
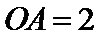
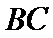
21．如图，在四棱锥中，底面四边长为的菱形，，，，为的中点，为的中点

（1）证明：直线；

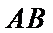
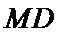
（2）求异面直线与所成角的大小。

正确答案

方法一（综合法）

（1）取OB中点E，连接ME，NE

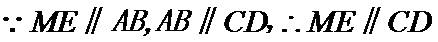
又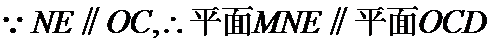

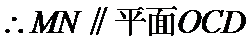
（2）

为异面直线与所成的角（或其补角）作连接

，

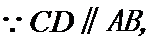
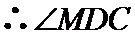
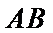
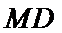
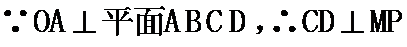
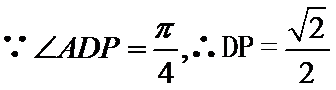
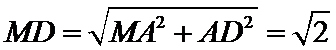
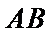
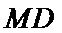
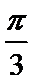
所以与所成角的大小为

方法二（向量法）作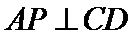于点P，

如图，分别以AB，AP，AO所在直线为轴建立坐标系，

，

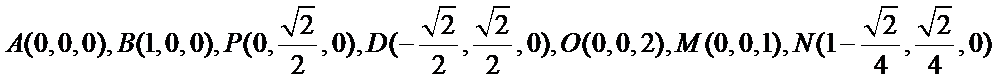
（1）

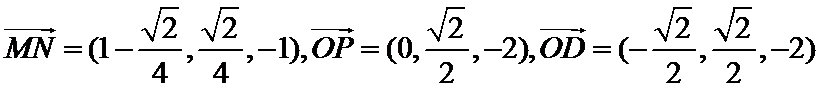
设平面OCD的法向量为，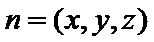

则

即

取，解得

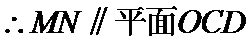
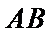
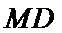
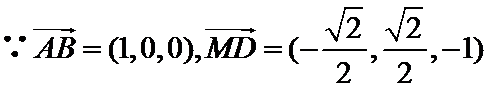
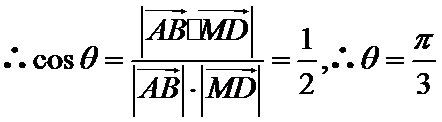
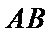
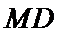
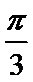
（2）设与所成的角为，

，

与所成角的大小为

解析

解析已在路上飞奔，马上就到！

知识点

异面直线及其所成的角直线与平面平行的判定与性质

题型：简答题

简答题 · 12 分

19．如图，已知四棱锥的底面是直角梯形，，，侧面底面，是的中点。

（1）求证：；

（2）求四棱锥的体积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质平面与平面垂直的判定与性质

题型：简答题

简答题 · 12 分

19. 如图所示，在棱长为2的正方体中，、分别为、的中点。

（Ⅰ）求证：//平面；

（Ⅱ）求证：；

（Ⅲ）求。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与直线垂直的判定与性质

题型：简答题

简答题 · 12 分

17．已知在四棱锥P - ABCD中，底面 ABCD是矩形，平面ABCD，AB= 2，PA=AD=1，E，F分别是AB、PD 的中点．

（1）求证：AF平面PDC；

（2）求三棱锥B-PEC的体积；

（3）求证：AF//平面PEC

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与平面垂直的判定与性质

继续学习学习下一知识点

下一知识点 : 直线、平面垂直的判定与性质

百度题库 > 高考 > 文科数学 > 直线、平面平行的判定与性质

扫码查看完整答案与解析