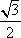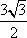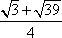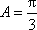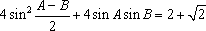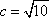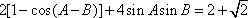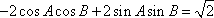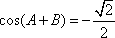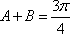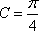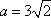- 余弦定理
- 共104题
在△ABC中,角A,B,C的对边分别为a,b,c,角A,B,C成等差数列。
(1)求cosB的值;
(2)边a,b,c成等比数列,求sinAsinC的值。
正确答案
(1) 
解析
(1)由已知2B=A+C,A+B+C=180°,解得B=60°,
所以
(2)解法一:由已知b2=ac,及
根据正弦定理得sin2B=sinAsinC,
所以sinAsinC=1-cos2B=
解法二:由已知b2=ac,及
根据余弦定理得
所以A=C=B=60°,故sinAsinC=
知识点
在△ABC中,AC=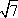
正确答案
解析
设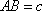
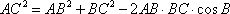
即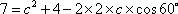
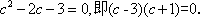
设BC边上的高等于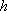
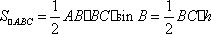
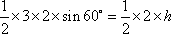
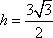
知识点
在△ABC中,角A,B,C所对的边分别为a,b,c. 已知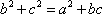
(1)求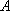
(2)如果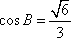
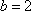

正确答案
(1)
(2)a=3
解析
(1)解:因为 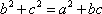
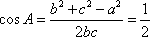
又因为 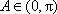
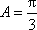
(2)解:因为 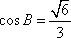
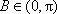
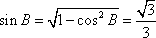
由正弦定理 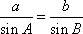
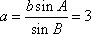
知识点
在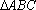
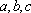
(1)求角C的大小;
(2)已知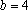


正确答案
(1)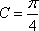
解析
(1)由已知得
化简得
故
所以
从而
(2)因为
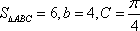
由余弦定理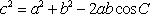
知识点
在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asin B=
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积。
正确答案
(1)
解析
(1)由2asin B=


因为A是锐角,所以
(2)由余弦定理a2=b2+c2-2bccos A,得b2+c2-bc=36.
又b+c=8,所以
由三角形面积公式S=
知识点
扫码查看完整答案与解析