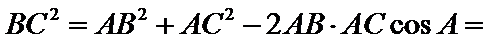余弦定理
共104题

· 余弦定理

余弦定理
共104题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

12．若锐角的面积为，且，则等于________．

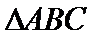
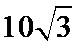
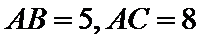
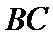
正确答案

解析

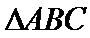
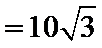
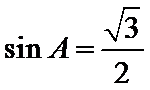
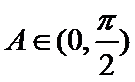
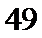
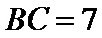
由已知得的面积为，所以，，所以．由余弦定理得，．

考查方向

1、三角形面积公式；2、余弦定理．

解题思路

利用三角形的面积公式求出A，再利用余弦定理求出BC.

易错点

计算能力弱，不会用余弦定理求三角形的面积

知识点

正弦定理余弦定理三角形中的几何计算

题型：填空题

填空题 · 5 分

9．在中，设分别为角的对边，若，，则边= ________.

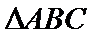
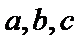
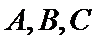
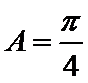
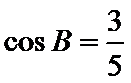
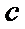
正确答案

解析

在三角形中，利用三角形的内角和A+B+C= 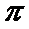，则可以求出SinC,然后利用正弦定理即可计算出=7.

考查方向

本题主要考查了解三角形中的正、余弦定理,在近几年的各省高考题出现的频率较高，常与三角恒等变形公式，等知识点交汇命题。

解题思路

画出草图，标出已知信息，根据已知元素，合理准确地使用正、余弦定理求解。

易错点

根据已知额信息，不能如何准确地使用正、余弦定理求解。

知识点

同角三角函数间的基本关系正弦定理余弦定理

题型：简答题

简答题 · 12 分

16．在△ABC中，角A，B，C的对边分别为a，b，c，向量和向量为共线向量．

（Ⅰ）求角的大小；

（Ⅱ）若a＝6，求△ABC面积的最大值．

正确答案

（1）；（2）。

解析

试题分析：本题属于向量结合三角函数以及解三角形的知识

（1）根据向量共线的坐标表示得到一个等式，再利用正弦定理实现边角互化从而可以解出角A；

（2）先由余弦定理再结合基本不等式即可。

（Ⅰ）因为向量和向量为共线向量，

所以，由正弦定理得，

即．

由于B是三角形的内角，，则，所以.

（Ⅱ）因为，

所以，

且仅当b=c时取得等号，所以，故，

所以当b＝c时，△ABC面积的最大值为

考查方向

本题考查了向量结合三角函数以及解三角形的知识。

解题思路

本题考查向量结合三角函数以及解三角形的知识，解题步骤如下：

（1）根据向量共线的坐标表示得到一个等式，再利用正弦定理实现边角互化从而可以解出角A；

（2）先由余弦定理再结合基本不等式即可。

易错点

不能联想到基本不等式。

知识点

正弦定理余弦定理三角形中的几何计算

题型：简答题

简答题 · 14 分

如图，在四边形中，=，且，，．

16.求的面积；

17.若，求的长．

第(1)小题正确答案及相关解析

正确答案

见解析

解析

（Ⅰ）

因为，所以，

所以△ACD的面积．

考查方向

本题考查余弦定理以及正弦定理的应用，属于中档题．

解题思路

利用已知条件求出∠D角的正弦函数值，然后求的面积；

易错点

主要易错于计算出错，

第(2)小题正确答案及相关解析

正确答案

见解析

解析

（Ⅱ）在△ACD中，，

所以．

在△ABC中，

把已知条件代入并化简得：因为，所以

考查方向

本题考查余弦定理以及正弦定理的应用，属于中档题．

解题思路

利用已知条件求出∠D角的正弦函数值，然后求的面积；

易错点

主要易错于计算出错，

题型：填空题

填空题 · 5 分

11．如图，在中，，，，则的值为________.

正确答案

解析

说明D在线段BC上，且是靠近B的一个三等分点，以向量, 为一组基底，表示出向量的数量积，即可算出的值为。

考查方向

本题主要考查了平面向量的数量积,在近几年的各省高考题出现的频率较高，常与三角恒等变形公式，向量的运算等知识点交汇命题。

解题思路

平面向量的数量积计算问题，往往有两种形式，一种是数量积的定义，而是利用数量积的坐标运算公式，涉及几何图形的问题，可利用几何性质用一组已知基底数量积表示所求数量积。

易错点

1、本题易直接使用数量积的定义，而不知如何计算夹角。

2、不会选择一组基底，从而用向量的加减运算及利用几何性质用一组已知基底数量积表示所求数量积。

知识点

余弦定理平面向量数量积的运算向量在几何中的应用

继续学习学习下一知识点

下一知识点 : 余弦定理的应用

百度题库 > 高考 > 文科数学 > 余弦定理

扫码查看完整答案与解析