热门试卷

某校从高一年级学生中随机抽取50名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：，得到如图所示的频率分布直方图.

（1）若该校高一年级共有学生1000人，试估计成绩不低于60分的人数；

（2）为了帮助学生提高数学成绩，学校决定在随机抽取的50名学生中成立“二帮一”小组，即从成绩中选两位同学，共同帮助中的某一位同学.已知甲同学的成绩为42分，乙同学的成绩为95分，求甲、乙恰好被安排在同一小组的概率.

              年月日，CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象，为了研究使用淡化海砂与混凝土耐久性是否达标有关，某大学实验室随机抽取了个样本，得到了相关数据如下表：

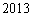
（1）根据表中数据，利用独立性检验的方法判断，能否在犯错误的概率不超过的前提下，认为使用淡化海砂与混凝土耐久性是否达标有关？

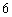
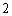
（2）若用分层抽样的方法在使用淡化海砂的样本中抽取了个，现从这个样本中任取个，则取出的个样本混凝土耐久性都达标的概率是多少？

参考数据：

某公司有男职员45名，女职员15名，按照分层抽样的方法组建了一个4人的科研攻关小组。

（1）求某职员被抽到的概率及科研攻关小组中男、女职员的人数；

（2）经过一个月的学习、讨论，这个科研攻关组决定选出两名职员做某项实验，方法是先从小组里选出1名职员做实验，该职员做完后，再从小组内剩下的职员中选一名做实验，求选出的两名职员中恰有一名女职员的概率；

（3）试验结束后，第一次做试验的职员得到的试验数据为68,70,71,72,74，第二次做试验的职员得到的试验数据为69,70,70,72,74，请问哪位职员的实验更稳定？并说明理由。

从某学校高三年级800名学生中随机抽取50名测量身高，据测量被抽取的学生的身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组，第二组；…第八组，下图是按上述分组方法得到的条形图.

（1）   根据已知条件填写下面表格：

（2）估计这所学校高三年级名学生中身高在以上（含）的人数；

（3）在样本中，若第二组有人为男生，其余为女生，第七组有人为女生，其余为男生，在第二组和第七组中各选一名同学组成实验小组，问：实验小组中恰为一男一女的概率是多少？

某中学在校就餐的高一年级学生有440名，高二年级学生有460名，高三年级学生有500名；为了解学校食堂的服务质量情况，用分层抽样的方法从中抽取70名学生进行抽样调查，把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级：1级（很不满意）；2级（不满意）；3级（一般）；4级（满意）；5级（很满意），其统计结果如下表（服务满意度为，价格满意度为）.

（1）求高二年级共抽取学生人数；

（2）求“服务满意度”为3时的5个“价格满意度”数据的方差；

（3）为提高食堂服务质量，现从且的所有学生中随机抽取两人征求意见，求至少有一人的“服务满意度”为1的概率.

国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”，方案要求以学校为单位组织实施，某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试，并对50分以上的成绩进行统计，其频率分布直方图如图所示，若90~100分数段的人数为2人.

（1）请求出70~80分数段的人数；

（2）现根据测试成绩从第一组和第五组（从低分段到高分段依次为第一组、第二组、…、第五组）中任意选出两人，形成搭档小组.若选出的两人成绩差大于20，则称这两人为“搭档组”，试求选出的两人为“搭档组”的概率.