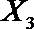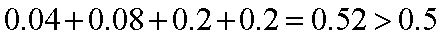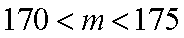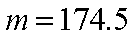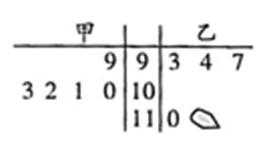- 统计与统计案例
- 共590题
20.对某校高三年级学生参加社区服务次数进行统计,随机抽取

(Ⅰ)求出表中

(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
正确答案
(Ⅰ)由分组

所以


所以
(Ⅱ)因为该校高三学生有240人,分组

所以估计在此区间内的人数为
(Ⅲ)这个样本参加社区服务的次数不少于20次的学生共有
设在区间



则任选


而两人都在

解析
解析已在路上飞奔,马上就到!
知识点
18.从某学校高三年级800我学生中随机抽取50名测量身高,据测量被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组


(1)根据已知条件填写下面的表格:
(2)估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数;
(3)在样本中,若第二组有1人为男生,其余为女生,第七组有1人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5。现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率。
正确答案
(1)由频率分布表得a+0.2+0.45+b+c=1, a+b+c=0.35
因为抽取的20件日用品中,等级系数为4的恰有3件,所以b=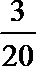
等级系数为5的恰有2件,所以c=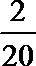
从而a=0.35-b-c=0.1
所以a=0.1 b=0.15 c=0.1
(2)从日用品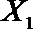
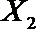
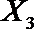
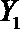
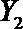
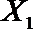
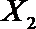
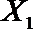

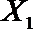
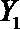
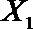
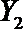
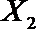
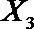
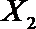
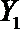
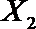
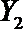
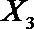
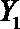
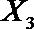
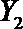
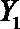
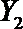
设事件A表示
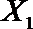
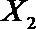
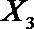
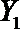
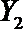
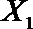
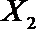
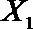
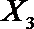
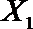
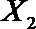
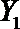
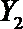
故所求的概率P(A)= 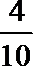
解析
解析已在路上飞奔,马上就到!
知识点
16. 某品牌汽车
已知分3期付款的频率为0.2,该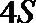
(Ⅰ)求上表中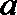
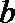
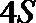
(Ⅱ)该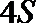
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
从某学校的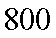
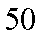
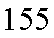
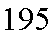
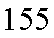
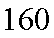
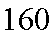
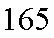
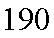
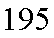
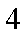
(1)求第七组的频率;
(2)估计该校的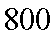
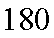
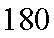
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为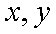
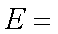
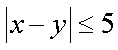
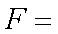
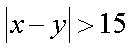

正确答案
见解析。
解析
(1)第六组的频率为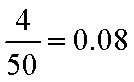
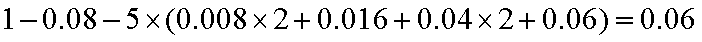
(2)身高在第一组[155,160)的频率为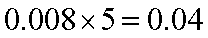
身高在第二组[160,165)的频率为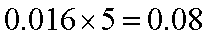
身高在第三组[165,170)的频率为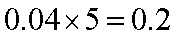
身高在第四组[170,175)的频率为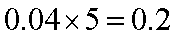
由于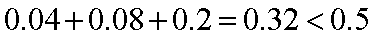
估计这所学校的800名男生的身高的中位数为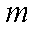
由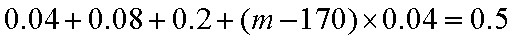
所以可估计这所学校的800名男生的身高的中位数为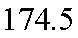
由直方图得后三组频率为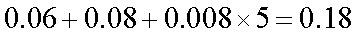
所以身高在180cm以上(含180cm)的人数为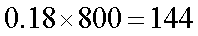
(Ⅲ)第六组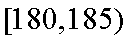
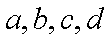
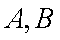
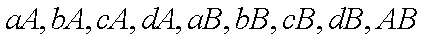
因事件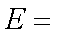
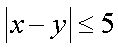
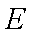
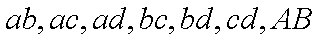
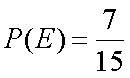
由于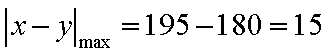
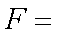
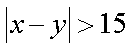
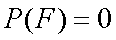
由于事件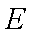
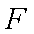
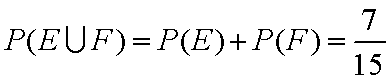
知识点
甲、乙两同学用茎叶图记录高三前5次数学测试的成绩,如图所示.他们在分析对比成绩变化时,发现乙同学成绩的一个数字看不清楚了,若已知乙的平均成绩低于甲的平均成绩,则看不清楚的数字为( )
正确答案
解析
本题考查茎叶图、平均数.甲的平均分为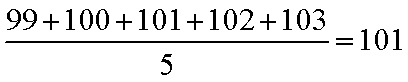
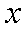
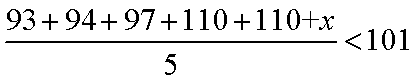
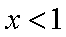
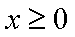
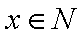
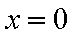
知识点
2014年“雾霾”成为年度关键词。雾霾天气是一种大气污染状态,雾霾是对大气中各种悬浮颗粒物含量超标的笼统表述,尤其是PM2.5日均值(微克/立方米)(空气动力学当量直径小于等于2.5微米的颗粒物)被认为是造成雾霾天气的“元凶”。 PM2.5日均值越小,空气质量越好。下面是国家环境标准设定的PM2.5日均值(微克/立方米)与空气质量等级对应关系如下表:
由全国重点城市环境监测网获得4月份某五天甲和乙城市的空气质量指数数据,用茎叶图表示如下:
(1)试根据上面的统计数据,分别计算两城市的PM2.5日均值的平均数,从计算结果看,哪个城市的空气质量较好?
(2) 试根据上面的统计数据,估计甲城市某一天空气质量等级为3级轻度污染的概率;
(3)分别从甲城市和乙城市的统计数据中任取一个,试求这两个城市空气质量等级相同的概率。
正确答案
(1)乙城市的空气质量较好(2)
解析
(1)乙城市的空气PM2.5日均值平均数为
甲城市的空气PM2.5日均值平均数为
乙城市的空气PM2.5日均值平均数小于甲城市,所以乙城市的空气质量较好。 ……3分
(2)根据上面的统计数据,可得在这五天中甲城市空气质量等级为3级轻度污染的频率为
则估计甲城市某一天的空气质量等级为3级轻度污染的概率为
(3)设事件A:从甲城市和乙城市的上述数据中分别任取一个,这两个城市的空气质量等级相同,由题意可知,从甲城市和乙城市的监测数据中分别任取一个,共有
(59,66),(59,68),(59,85),(59,88)(59,98)
(83,66),(83,68),(83,85),(83,88)(83,98)
(87,66),(87,68),(87,85),(87,88)(87,98)
(95,66),(95,68),(95,85),(95,88)(95,98)
(116,66),(116,68),(116,85),(116,88)(116,98) …………9分
其数据表示两城市空气质量等级相同的包括同为2级良的为甲59,乙66,乙68;同为3级轻度污染的为甲83,甲87,甲95; 乙85,乙88,乙98;则空气质量等级相同的为:
(59,66),(59,68),
(83,85),(83,88),(83,98),
(87,85),(87,88),(87,98),
(95,85),(95,88),(95,98),。共11个结果. ………11分
所以这两个城市空气质量等级相同的概率为
知识点
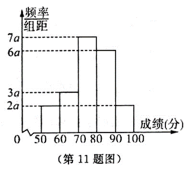
100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则模块测试成绩落在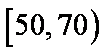
正确答案
25
解析
略
知识点
对某校高一年级学生参加社区服务次数进行统计,随机抽取


(1)求出表中M、p及图中a的值;
(2)若该校高一学生有360人,试估计他们参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,25)内的概率。
正确答案
(1)M=40,a=0.125,p=0.075
(2)225
(3)
解析
(1)由题可知



又 



则

(2)参加在社区服务次数在区间

(3)在样本中,处于








知识点
19.某学校为了了解高三学生的身体健康状况,在该校高三年级学生中随机抽取了100名学生进行调查,按日睡眠时间(单位:小时)分组得到如图1的频率分布表和如图2的频率分布直方图。
(Ⅰ)请补全频率分布直方图,并求频率分布表中的a,b;
(Ⅱ)现用分层抽样法从第一、二、五组中抽取6名学生进行体检,求第一、二、五组各应抽取多少名学生?
(III)在上述6名学生中随机抽取2名学生进行某专项体检,求这2名学生中恰有一名学生在第二组的概率。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析