- 统计与统计案例
- 共590题
9.下列说法中正确的有( )
正确答案
解析
一组数据的平均数介于这组数据中的最大数据与最小数据之间,所以A错;众数是一组数据中出现最多的数据,所以可以不止一个,B错;若一组数据的个数有偶数个,则其中中位数是中间两个数的平均值,所以不一定是这组数据中的某个数据,C错;一组数据的方差越大,说明这组数据的波动越大,D对.
知识点
某工厂有甲、乙两个生产小组,每个小组各有四名工人,某天该厂每位工人的生产情况如下表。
(1)用茎叶图表示两组的生产情况;
(2)求乙组员工生产件数的平均数和方差;
(3)分别从甲、乙两组中随机选取一名员工的生产件数,求这两名员工的生产总件数为19的概率。
(注:方差

正确答案
见解析。
解析
(1)茎叶图:
(2)所以平均数为
方差为
s2=
(3)记甲组四名员工分别为A1,A2,A3,A4,他们生产的产品件数依次为9,9,11,11;乙组四名员工分别为B1,B2,B3,B4,他们生产的产品件数依次为9,8,9,10.
分别从甲、乙两组中随机选取一名员工,所有可能的结果有16个,它们是:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A3,B2),(A3,B3),(A3,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4)。
用C表示:“选出的两名员工的生产总件数为19”这一事件,则C中的结果有4个,它们是:(A1,B4),(A2,B4),(A3,B2),(A4,B2),故所求概率为
知识点
近年来,我国许多地方出现雾霾天气,影响了人们的出行、工作与健康,其形成与


某环保部门为了了解甲、乙两市的空气质量状况,在某月中分别随机抽取了甲、乙两市6天的
(1)求甲、乙两市
(2)若从甲市这6天的样本数据中随机抽取两天的数据,求恰有一天空气质量等级为一级的概率。
正确答案
见解析
解析
(1)甲市抽取的样本数据分别是32,34,45,56,63,70;乙市抽取的样本数据为33,46,47,51,64,71.


因为
(2)由茎叶图知,甲市6天中有2天空气质量等级为一级,有4天空气质量等级为二级,空气质量等级为二级的4天数据为


记“恰有一天空气质量等级为一级”为事件A,则事件A包含的基本事件为:
所以

知识点
对某商店一个月内每天的顾客人数进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数、众数、极差分别是 ( )
正确答案
解析
由茎叶图易知:中位数为46,该样本出现次数最多的数为45,最大的数为68,最小的数为12,所以级差为56。
知识点
6. 从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图3,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.
(1)求

(2)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.某一个班全体学生参加历史测试,成绩的频率分布直方图如图,则该班的平均分估计是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.给出下列四个命题:
①函数f(x)=ex+ e-x有最小值2;
②函数f(x)=4sin(2x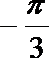
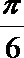
③一组数据的平均数一定不小于它的中位数;
④已知定义在R上的可导函数y=f(x)满足:对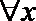
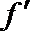
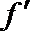
其中正确命题的序号是__________.(写出所有正确命题的序号)
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
18.某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔一小时抽一包产品
(1)根据样本数据,计算甲、乙两个车间产品重量的均值与方差,
(2)若从乙车间6件样品中随机抽取两件,求所抽取两件样品重量之差不超过2克的概率.
正确答案
(1)甲相对稳定。


(2)从乙车间6件样品中随机抽取两件,共有15种不同的取法:(108,109),
(108,110),(108,112),(108,115),(108,124),(109,110),
(109,112),(109,115),(109,124),(110,112),(110,115),
(110,124),(112,115),(112,124),(115,124).
设A表示随机事件“所抽取的两件样品的重量之差不超过2克”,
则A的基本事件有4种:(108,109),(108,110),(109,110),(110,112).
故所求概率为P(A)=
解析
解析已在路上飞奔,马上就到!
知识点
9.一个样本容量为20 的样本,它的数据组成一个公差不为0 的等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析















