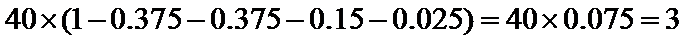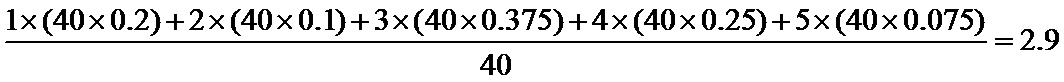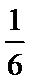统计与统计案例_章节学习

1

题型：简答题

|

简答题 · 12 分

16.我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行了调查，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5）， [0.5,1），……[4,4.5]分成9组，制成了如图所示的频率分布直方图。

（I）求直方图中的a值；

（II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数．说明理由；

（Ⅲ）估计居民月均用水量的中位数.

正确答案

知识点

频率分布直方图众数、中位数、平均数随机抽样和样本估计总体的实际应用

1

题型：填空题

|

填空题 · 5 分

13.中位数为1010的一组数构成等差数列，其末项为2015，则该数列的首项为________.

正确答案

5

解析

若这组数有个，则，，又，所以；若这组数有个，则，，又，所以；故答案为5

考查方向

等差数列与等比数列性质的应用

解题思路

本题考查等差数列的性质，这组数字有可能是偶数个，也有可能是奇数个.然后利用等差数列性质.

易错点

注意运算的准确性．

知识点

众数、中位数、平均数

1

题型：简答题

|

简答题 · 12 分

某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．

18.求直方图中的值；

19.求月平均用电量的众数和中位数；

20.在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？

第(1)小题正确答案及相关解析

正确答案

（1）；

解析

（1）由，得，，所以直方图中的值是。

考查方向

本题考察了频率分布直方图以及样本的数字特征、分层抽样等知识，属于中等题。

解题思路

由频率之和等于1，求出的值。

易错点

用频率分布直方图估算样本数字特征的公式，计算。

第(2)小题正确答案及相关解析

正确答案

（2），；

解析

（2）月平均用电量的众数是

因为，所以月平均用电量的中位数在内，设中位数为，由得：，所以月平均用电量的中位数是

考查方向

本题考察了频率分布直方图以及样本的数字特征、分层抽样等知识，属于中等题。

解题思路

由最高矩形的横坐标中点可得众数，由频率之和等于，则可得中位数。

易错点

用频率分布直方图估算样本数字特征的公式，计算。

第(3)小题正确答案及相关解析

正确答案

（3）．

解析

（3）月平均用电量为的用户有户，月平均用电量为的用户有户，月平均用电量为的用户有户，月平均用电量为的用户有户，抽取比例，所以月平均用电量在的用户中应抽取户。

考查方向

本题考察了频率分布直方图以及样本的数字特征、分层抽样等知识，属于中等题。

解题思路

先计算出月平均用电量为的用户的户数，再计算抽取比例，进而可得月平均用电量在的用户中应抽取的户数。

易错点

用频率分布直方图估算样本数字特征的公式，计算。

1

题型：填空题

|

填空题 · 5 分

13.如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩（单位：环），若两位运动员平均成绩相同，则成绩较为稳定（方差较小）的那位运动员成绩的方差为________.

正确答案

2

解析

，

∴

考查方向

本题主要考查了茎叶图

解题思路

根据茎叶图，先求出x，再根据方差公式进行求解．

易错点

本题易在茎叶图上容易读错，要区分方差与标准差

知识点

茎叶图众数、中位数、平均数极差、方差与标准差

1

题型：简答题

|

简答题 · 12 分

18．截至2014年11月27目，我国机动车驾驶人数量突破3亿大关，年均增长超过两千万．为了解某地区驾驶预考人员的现状，选择A，B,C三个驾校进行调查．参加各驾校科目一预考人数如下：

若用分层抽样的方法从三个驾校随机抽取24人进行分析，他们的成绩如下：

（I）求三个驾校分别应抽多少人?

（II）补全下面的茎叶图，并求样本的众数和极差；

(Ⅲ)在对数据进一步分析时，满足｜x－96．5｜≤4的预考成绩，称为具有M特性．在样本中随机抽取一人，求此人的预考成绩具有M特性的概率．

正确答案

（1）6,8,10；（2）众数为：92，极差为：99-64=35；（3）P(A)= 。

解析

试题分析：本题属于分层抽样和古典概型，

（1）利用分层抽样也就是按比例抽样计算即可；

（2）按步骤直接计算；

（3）利用古典概型公式来计算。

考查方向

本题考查了分层抽样和古典概型。

解题思路

本题考查分层抽样和古典概型，解题步骤如下：

（1）利用分层抽样也就是按比例抽样计算即可；

（2）按步骤直接计算；

（3）利用古典概型公式来计算。

易错点

计算出错。

知识点

茎叶图众数、中位数、平均数

1

题型：简答题

|

简答题 · 12 分

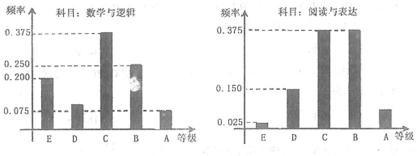
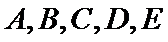
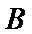
在某大学自主招生考试中，所有选报II类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试，成绩分别为五个等级．某考场考生的两科考试成绩的数据统计如下图所示，其中“数学与逻辑”科目的成绩为的考生有10人．

19.求该考场考生中“阅读与表达”科目中成绩为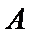的人数；

20.若等级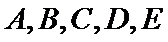分别对应5分，4分，3分，2分，1分，求该考场考生“数学与逻辑”科目的平均分；

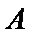
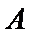
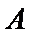
21.已知参加本考场测试的考生中，恰有两人的两科成绩均为，以在至少一科成绩为的考生中，随机抽取两人进行访谈，求这两人的两科成绩均为的概率．

第(1)小题正确答案及相关解析

正确答案

（1）3；

解析

（1）因为“数学与逻辑”科目中成绩等级为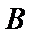的考生有10人，

所以该考场有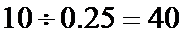人　所以该考场考生中“阅读与表达”科目中成绩等级为的人数

考查方向

本题主要考查频率分布直方图、古典概型等知识，意在考查考生的理解能力和应用能力。

解题思路

先根据频率分布直方图求出第（1）问；

易错点

对于题中给出的信息不理解或理解错误；

第(2)小题正确答案及相关解析

正确答案

；

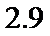
解析

（2）该考场考生“数学与逻辑”科目的平均分为

考查方向

本题主要考查频率分布直方图、古典概型等知识，意在考查考生的理解能力和应用能力。

解题思路

根据第（1）问的结果估和频率分布直方图估计该考场考生“数学与逻辑”科目的平均分；

易错点

不会根据频率分布直方图估计平均值。

第(3)小题正确答案及相关解析

正确答案

（3）

解析

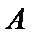
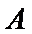
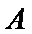
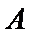
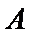
（3）因为两科考试中，共有6人得分等级为，又恰有两个的两科成绩等级均为，所以还有2人只有一个科目得分为．设这四人为甲，乙，丙，丁，其中甲，乙是两科成绩都是的同学，则在至少一科成绩等级为的考生中，随机抽取两人进行访谈，基本事件空间为

1个，则

考查方向

本题主要考查频率分布直方图、古典概型等知识，意在考查考生的理解能力和应用能力。

解题思路

按照古典概型求概率的过程求解即可。

易错点

对于题中给出的信息不理解或理解错误

1

题型：单选题

|

单选题 · 5 分

8.已知下列三个命题：

①若两组数据的平均数相等，则它们的标准差也相等；

②在区间上随机选取一个数x，则的概率为；

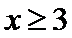
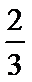
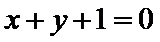
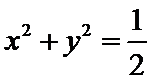
③直线与圆相切；

其中真命题的个数是（）

A0

B1

C2

D3[

正确答案

B

解析

1）根据平均数、方差与标准差的性质可知①错误

2）根据与长度有关的几何概型可知正确为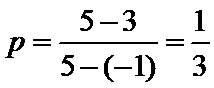 ∴②错误

3）根据直线与圆的位置关系，圆心到直线的距离为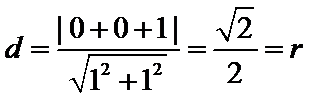所以③正确

∴ 选B

考查方向

本题主要考察了平均数、方差与标准差，考察了与长度、角度有关的几何概型，考察了直线与圆的位置关系，

解题思路

直接法对每一个判断

1）根据平均数、方差与标准差的性质可知①错误

2）根据与长度有关的几何概型可知正确为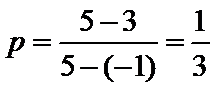 ∴②错误

3）根据直线与圆的位置关系，圆心到直线的距离为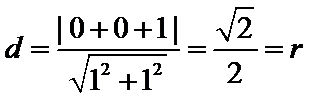所以③正确

易错点

本题属于数学中的多选题，易错于对个别判断错误导致选择错误，

知识点

随机事件的频率与概率众数、中位数、平均数极差、方差与标准差

1

题型：简答题

|

单选题

哮病发生的“夙根”是

A．风
B．痰
C．气
D．虚
E．淤

正确答案

B

解析

暂无解析

1

题型：单选题

|

单选题 · 5 分

4．重庆市2013年各月的平均气温（°C）数据的茎叶图如下

则这组数据中的中位数是（）

A19

B20

C21.5

D23

正确答案

B

解析

由茎叶图可知总共12个数据，处在正中间的两个数是第六和第七个数，它们都是20，由中位数的定义可知：其中位数就是20，故选B.

考查方向

本题主要考查茎叶图的应用，根据中位数的定义是解决本题的关键．比较基础．

解题思路

本题考查复数的概念和运算，采用分母实数化和利用共轭复数的概念进行化解求解.

易错点

本题属于基础题，注意运算的准确性.

知识点

众数、中位数、平均数

1

题型：简答题

|

简答题 · 12 分

18.某车间将10名技工平均分为甲，乙两组加工某种零件，在单位时间内每个技工加工零件若干，其中合格零件的个数如下表：

（1）分别求出甲，乙两组技工在单位时间内完成合格零件的平均数及方差，并由此分析两组技工的技术水平；

（2）质检部门从该车间甲，乙两组中各随机抽取1名技工，对其加工的零件进行检测，若两人完成合格零件个数之和超过12件，则称该车间“质量合格”，求该车间“质量合格”的概率.

正确答案

（1）依据题中的数据可得，

X甲= S2甲=5.2X乙= S2乙=2

所以两组技工的总体水平相同，甲组中技工的技术水平差异比乙组大。

（2）设事件A表示：该车间“质量合格”，

则从甲、乙两组中各抽取1名技工完成合格零件个数的基本事件为：（4，5）（4，6）（4，7）（4，8）（4，9）（5，5）（5，6）（5，7）（5，8）（5，9）（7，5）(7,6)(7,7)(7,8)(7,9)(9,5)(9,6)(9,7)(9,8)(9,9)(10,5)(10,6)(10,7)(10,8)(10,9)共25种，

所以概率P(A)= 17/25

解析

利用平均数和方差公式，求得甲的平均数是7，乙的平均数是7，甲的方差为5.2，乙的方差为2，两组技工的总体水平相同，甲组中技工的技术水平差异比乙组大；列出所有时间发生的基本事件，共17种，所以质量合格的概率为17/25

考查方向

本题主要考查平均数与方差的求法。考查随机事件发生的概率

解题思路

按照概念依次求解

易错点

对平均数和方差理解不透彻，不会计算随机事件发生的概率

知识点

古典概型的概率众数、中位数、平均数极差、方差与标准差

热门试卷

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点