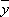- 统计与统计案例
- 共590题
13.如图茎叶图记录了甲、乙
正确答案
2
解析
∴
考查方向
解题思路
根据茎叶图，先求出x，再根据方差公式进行求解．
易错点
本题易在茎叶图上容易读错，要区分方差与标准差
知识点
8.已知下列三个命题：
①若两组数据的平均数相等，则它们的标准差也相等
②在区间
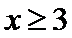
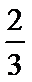
③直线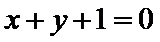
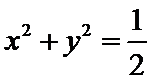
其中真命题的个数是（ ）
正确答案
解析
1）根据平均数、方差与标准差的性质可知①错误
2）根据与长度有关的几何概型可知正确为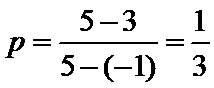
3）根据直线与圆的位置关系，圆心到直线的距离为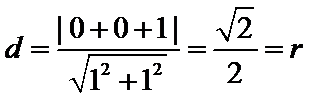
∴ 选B
考查方向
解题思路
直接法对每一个判断
1）根据平均数、方差与标准差的性质可知①错误
2）根据与长度有关的几何概型可知正确为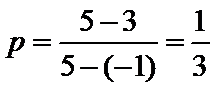
3）根据直线与圆的位置关系，圆心到直线的距离为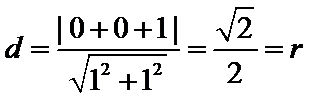
易错点
本题属于数学中的多选题，易错于对个别判断错误导致选择错误，
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
根据如下样本数据：
得到回归方程为
正确答案
解析
样本平均数
∴
∴a=0.25﹣（﹣1.4）•5.5=7.95
知识点
已知回归直线的斜率的估计值是
A
B
C
D
正确答案
解析
略
知识点
下列结论：
①直线a,b为异面直线的充要条件是直线a,b不相交；
②从总体中抽取的样本（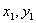
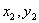
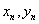
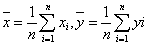
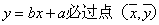
③函数
④已知函数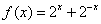
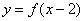
其中正确的结论是 .（注：把你认为正确结论的序号都填上）
正确答案
②④
解析
略
知识点
设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为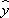
Ay与x具有正的线性相关关系
B回归直线过样本点的中心（
C若该大学某女生身高增加1cm，则其体重约增加0.85kg
D若该大学某女生身高为170cm，则可断定其体重必为58.79kg
正确答案
解析
由回归方程为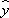
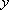
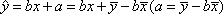
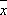
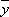
知识点
已知
假设根据上表数据所得线性回归直线方程为
A
B
C
D
正确答案
解析
本题考查的是线性回归方程，画出散点图，可大致的画出两条直线（如图），由两条直线的相对位置关系可判断
知识点
18.某车间将10名技工平均分为甲，乙两组加工某种零件，在单位时间内每个技工加工零件若 干，其中合格零件的个数如下表：
（1）分别求出甲，乙两组技工在单位时间内完成合格零件的平均数及方差，并由此分析两组技工的
（2）质检部门从该车间甲，乙两组中各随机抽取1名技工，对其加工的零件进行检测，若两人完成合格零件个数之和超过12件，则称该车
正确答案
（1）依据题中的数据可得，
X甲=
所以两组技工的总体水平相同，甲组中技工的技术水平差异比乙组大。
（2）设事件A表示：该车间“质量合格”，
则从甲、乙两组中各抽取1名技工完成合格零件个数的基本事件为：（4，5）（4，6）（4，7）（4，8）（4，9）（5，5）（5，6）（5，7）（5，8）（5，9）（7，5）(7,6)(7,7)(7,8)(7,9)(9,5)(9,6)(9,7)(9,8)(9,9)(10,5)(10,6)(10,7)(10,8)(10,9)共25种，
所以概率P(A)= 17/25
解析
利用平均数和方差公式，求得甲的平均数是7，乙的平均数是7，甲的方差为5.2，乙的方差为2，两组技工的总体水平相同，甲组中技工的技术水平差异比乙组大；列出所有时间发生的基本事件，共17种，所以质量合格的概率为17/25
考查方向
本题主要考查平均数与方差的求法。考查随机事件发生的概率
解题思路
按照概念依次求解
易错点
对平均数和方差理解不透彻，不会计算随机事件发生的概率
知识点
4.若样本数据
正确答案
16
解析
2*8=16
考查方向
解题思路
本题考查采用标准差与数据关系的结论：只与系数相关。解题步骤如下：2*8=16
易错点
本题必须注意标准差含义，忽视则会出现错误。
知识点
扫码查看完整答案与解析