- 统计与统计案例
- 共590题
16.我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行了调查，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5）， [0.5,1），……[4,4.5]分成9组，制成了如图所示的频率分布直方图。
（I）求直方图中的a值；
（II）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数．说明理由；
（Ⅲ）估计居民月均用水量的中位数.
正确答案
知识点
3.某校高三年级共有学生900人，编号为1,2,3，……，900，现用系统抽样的方法抽取一个容量为45的样本，则抽取的45人中，编号落在区间
正确答案
解析
抽样比是20，然后在要求的区间上的人数为240/20=12人，所以选C。
【修改点】增加了区间
考查方向
解题思路
先算出抽样比，在算出要求的区间所占的人数。
易错点
不理解系统抽样的概念。
知识点
5．已知具有线性相关关系的两个变量
且回归直线方程为
A
B
C
D
正确答案
解析
由题意可得，
考查方向
解题思路
1.先求出样本点的中心
易错点
1.不理解回归直线部分的基础知识，导致不知道该干什么；2.数据计算出错。
知识点
4．以下四个命题：其中真命题为( )
①从匀速传递的产品生产流水线上，质检员每20分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②两个随机变量相关性越强，则相关系数的绝对值越接近于1；
③在回归直线方程
④对分类变量X与Y，它们的随机变量K2的观测值k来说，k越小，“X与Y有关系”的把握程度越大．
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
根据如下样本数据：
得到回归方程为
正确答案
解析
样本平均数
∴
∴a=0.25﹣（﹣1.4）•5.5=7.95
知识点
已知回归直线的斜率的估计值是
A
B
C
D
正确答案
解析
略
知识点
下列结论：
①直线a,b为异面直线的充要条件是直线a,b不相交；
②从总体中抽取的样本（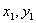
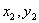
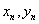
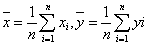
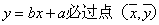
③函数
④已知函数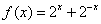
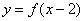
其中正确的结论是 .（注：把你认为正确结论的序号都填上）
正确答案
②④
解析
略
知识点
设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为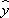
Ay与x具有正的线性相关关系
B回归直线过样本点的中心（
C若该大学某女生身高增加1cm，则其体重约增加0.85kg
D若该大学某女生身高为170cm，则可断定其体重必为58.79kg
正确答案
解析
由回归方程为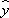
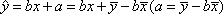
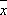
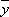
知识点
已知
假设根据上表数据所得线性回归直线方程为
A
B
C
D
正确答案
解析
本题考查的是线性回归方程，画出散点图，可大致的画出两条直线（如图），由两条直线的相对位置关系可判断
知识点
扫码查看完整答案与解析