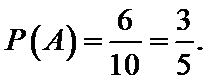- 统计与统计案例
- 共590题
为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:
19.由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
20.若对年龄在[5,15)的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?

正确答案
见解析
解析
解:(Ⅰ)2乘2列联表
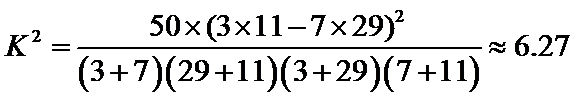
所以没有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异.
考查方向
解题思路
本题的解题思路
1)根据题意填写表格,并计算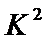
2)对年龄在[5,15)进行区分和分类,写出所有可能
3)利用古典概型求出概率值
易错点
本题第一问易错于计算出错。第二问基本事件空间漏或者重复出错
正确答案
见解析
解析
解:
(Ⅱ)设年龄在[5,15)中支持“生育二胎”的4人分别为a,b,c,d, 不支持“生育二胎”的人记为M,
则从年龄在[5,15)的被调查人中随机选取两人所有可能的结果有:(a,b), (a,c), (a,d), (a, M), (b,c), (b,d),(b, M), (c, d), (c, M),(d, M).
设“恰好这两人都支持“生育二胎””为事件A,
则事件A所有可能的结果有:(a,b), (a,c), (a,d), (b,c), (b,d), (c, d),
∴
所以对年龄在[5,15)的被调查人中随机选取两人进行调查时,恰好这两人都支持“生育二胎”的概率为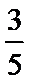
考查方向
解题思路
本题的解题思路
1)根据题意填写表格,并计算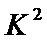
2)对年龄在[5,15)进行区分和分类,写出所有可能
3)利用古典概型求出概率值
易错点
本题第一问易错于计算出错。第二问基本事件空间漏或者重复出错
19.有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
已知在全部105人中抽到随机抽取1人为优秀的概率为
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,若按
(Ⅲ)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
参考公式:
参考数据:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸,呼吸困难等心肺疾病,为了解某市心肺疾病是否与性别有关,在某医院随机对入院50人进行了问卷调查,得到了如下的列联表.
(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(Ⅱ)在上述抽取的6人中选2人,求恰有一名女性的概率;
(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量
下面的临界值表供参考:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.某人研究中学生的性别与阅读量的关系,随机抽查500名中学生,得到统计数据如下表:
附表:
参照附表,可得到的结论是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.某研究小组随机在高二学生中抽查了105名学生,以研究他们的数学成绩与物理成绩的联系,得到如图2×2列联表:
则数学成绩与物理成绩之间有关系的可能性为( )
正确答案
解析
知识点
7.某研究小组随机在高二学生中抽查了105名学生,以研究他们的数学成绩与物理成绩的联系,得到如图2×2列联表:
则数学成绩与物理成绩之间有关系的可能性为( )
正确答案
解析
知识点
“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动,假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(1)若某参与者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(2)为了解冰桶挑战赛与受邀者的性别是否有关,某调查机构

根据表中数据,能否有90%的把握认为“冰桶挑战赛与受邀者的性别有关”?
附:
正确答案
见解析
解析
(1)这3个人接受挑战分别记为

这3个人参与该项活动的可能结果为:







其中,至少有2个人接受挑战的可能结果有:




(2)根据


因为
知识点
大家知道,莫言是中国首位获得诺贝尔奖的文学家,国人欢欣鼓舞.某高校文学社从男女生中各抽取50名同学调查对莫言作品的了解程度,结果如下:
(1)试估计该校学生阅读莫言作品超过50篇的概率;
(2)对莫言作品阅读超过75篇的则称为“对莫言作品非常了解”,否则为“一般了解”。根据题意完成下表,并判断能否有75%的把握认为对莫言作品的非常了解与性别有关?
附:
正确答案
见解析。
解析
(1)由抽样调查阅读莫言作品在50篇以上的频率为

(2)
根据列联表数据得

所以没有75%的把握认为对莫言作品的非常了解与性别有关.
知识点
17.某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有


(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下
①完成列联表;
②能否有
(3)若一班有





现从这
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.第12届全国人民代表大会于2013年3月在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和1 4名女记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语.
(I)根据以上数据完成以下2×2列联表:
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
参考公式:
参考数据:
(II)会俄语的6名女记者中有4人曾在俄罗斯工作过,若从会俄语的6名女记者中随机抽取2人做同声翻译,则抽出的2人都在俄罗斯工作过的概率是多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析