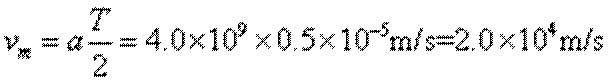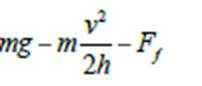- 动能 动能定理
- 共113题
如图所示,一质量m=0.4 kg的滑块(可视为质点)静止于动摩擦因数μ=0.1的水平轨道上的A点.现对滑块施加一水平外力,使其向右运动,外力的功率恒为P=10.0 W.经过一段时间后撤去外力,滑块继续滑行至B点后水平飞出,恰好在C点以5m/s的速度沿切线方向进入固定在竖直平面内的光滑圆弧形轨道,轨道的最低点D处装有压力传感器.已知轨道AB的长度L=2.0 m,半径OC和竖直方向的夹角α=37°,圆形轨道的半径R=0.5 m.(空气阻力可忽略,重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8),求:
28.滑块运动到D点时压力传感器的示数;
29.水平外力作用在滑块上的时间t.
正确答案
25.6 N
解析
(1)滑块由C点运动到D点的过程,由机械能守恒定律得:

考查方向
解题思路
(1)根据机械能守恒定律求出滑块运动到D点的速度
易错点
物体运动过程的分析,圆周运动最低点向心力的确定,平抛运动规律的应用,A到B合外力做功的计算。
正确答案
0.4s
解析
滑块运动到B点的速度为:

考查方向
解题思路
根据牛顿第二定律求滑块运动到D点时压力传感器的示数;将C点的速度分解为水平方向和竖直方向,结合平行四边形定则求出水平分速度,即得B点的速度。对A到B的过程运用动能定理求出外力作用的时间。
易错点
物体运动过程的分析,圆周运动最低点向心力的确定,平抛运动规律的应用,A到B合外力做功的计算。
有一半径为R=0.4m的光滑半圆轨道,直径BC竖直,与粗糙水平面相切于B点,如图所示。在距B点s=2.1m的A点有一质量为m=0.2kg的小滑块,小滑块与水平面间的动摩擦因数μ = 0.5,在与水平方向成α=53º的恒力F的

24.小滑块运动到C点时速度的大小?
25.小滑块运动到圆轨道的B点,撤去F时受到轨道的支持力为多大?
26.恒力F的大小?
正确答案
解析
(1)在C点:

考查方向
考查物体做圆周运动向心力的分析,及其与速度的关系公式:
解题思路
分析物体在C点的受力,得出合外力,根据合外力提供向心力 
易错点
对向心力由什么力提供容易模糊不清。
正确答案
(2)12.5N
解析
(2)在从B到C的过程中,由机械能守恒定律可知


考查方向
考查根据动能动能定理求速度:
解题思路
根据B到C过程中动能定理的公式解得物体在B点的速度,根据速度与向心力、合外力
易错点
对向心力由什么力提供容易模糊不清。
正确答案
(3)2N
解析
在从A到B的过程中

考查方向
考查牛顿第二运动定律:F合力=ma。考查运动学的基本公式:
解题思路
对A到B的过程中使用动能定理解得恒力F的大小,或者根据运动学公式求出加速度a,再根据匀速运动的条件(受力平衡) 求解恒力F的大小。
易错点
对向心力由什么力提供容易模糊不清。
如图甲所示,M、N 为一对竖直放置的平行金属板,中心各有一小孔 P 和 Q,PQ 连线 垂直金属板,现有质量 m=2.0×10-27 kg,电荷量 q=1.6×10-19C 带正电的粒子连续不断地从 小孔 P 飘入 M、N 板之间,带电粒子在小孔 P 处的初速可忽略。在 M、N 间加有如图乙所 示的交变电压,且 t=0 时 M 板电势高于 N 板电势。带电粒子在 M、N 间运动过程中,粒子 所受重力以及粒子之间的相互作用力均可忽略不计。
28.如果两平行金属板间距离 d=5.0cm, 求:
①带电粒子从小孔 Q 中射出时的最大速度值;
② 在 t=0.125×10
29.如果在
正确答案
(1)①
解析
(1)带电粒子在电场中运动的加速度
①带电粒子经过半个周期加速运动,前进的距离
②在t=0.125×10-5s时刻飘入P孔的带电粒子,在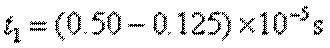


解得EkQ=5.0×10-20J
考查方向
解题思路
(1)进入到金属板之间的带电粒子的加速度根据牛顿第二定律和
结合求解.再由Vm=at即可求出最大速度。
易错点
此题很难,每个点都容易出错。
正确答案
(2)d<2.5cm
解析
(2)如果只在[n~(n+0.25)]×10-5s内,
即在每个周期的
只要每个周期内
则在每个周期内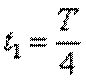
每个周期内
在
在
所以,
在每个周期内
在
并可从小孔Q中射出,
则两板间距离d应满足的条件是
解得 s =2.5cm 即两板间距离d应满足的条件是d<2.5cm
考查方向
解题思路
(2)通过分析每个周期内带电粒子的运动情况,确定只有在每个周期的0~
时间内放出的带电粒子才能从小孔Q中射出时应满足的条件,根据牛顿第二定律和运动学公式求解各物理量之间应满足的关系.
易错点
此题很难,每个点都容易出错。
20.如图所示,可视为质点的质量为m且所带电量为q的小球,用一绝缘轻质细绳悬

正确答案
解析
因为在小球在运动过程中电场力做了功,所以机械能不守恒,故A错误,B正确;
小球在运动过程中电场力







考查方向
解题思路
1、根据机械能守恒定律的条件判定是否守恒。
2、找出电场力和重力的合力的大小方向,将电场和重力场等效,在等效场的最高点速度最小,根据动能定理求出最小速度。
易错点
本题的易错点就是以为在竖直最高点速度最小。
知识点
4.如图是某种电磁泵模型,泵体是一个长方体,ab边长为L1,左右两侧面是边长为L2的正方形,泵体处在垂直向外、磁感应强度为B的匀强磁场中,泵体上下表面接电动势为U的电源(内阻不计)。若泵工作时理想电流表示数为I,泵和水面高度差为h,液体的电阻率为ρ,t时间内抽取液体的质量为m,不计液体在流动中和管壁之间的阻力,重力加速度为g.则( )
正确答案
解析
本题是电磁感应现象中,通电导体在电场中受安培力运动的问题,较为基础,但模型理解起来有些不易
A选项,由电磁驱动可知,通电直导线在磁场中受安培力作用,并可以在其作用下运动。根据左手定则可知,安培力向左则需要电流向下,上表面为电源正极。错误
B选项,磁场作用下的电流的有效长度为L2。错误
C选项,电源提供的电功率为

D选项,电流做功过程中重力做负功,电流产热消耗能量,其余为液体动能。正确
考查方向
解题思路
根据题意可知本题是电磁驱动的基本内容,通电直导线在磁场中受安培力作用,并可以在其作用下运动。根据左手定则可知,安培力向左则需要电流向下,上表面为电源正极,且磁场作用下的电流的有效长度为L2。电源提供的电功率为

易错点
不能准确把握本题的考察模型,导电液体在安培力的作用下运动,以及在运动过程中损失的能量。
知识点
9.如图,水平转台上有一质量为m的物块,用长为L的细绳将物块连接在转轴上,细
线与竖直转轴夹角为θ角,此时绳中张力为零,物块与转台间动摩擦因数为μ(μ
正确答案
解析
A选项,对物体受力分析可知物体离开元盘前,

C选项,由转台对物体无支持力可知,仅有重力拉力提供圆周运动向心力

D选项,根据物体转动角速度可知,物体已脱离水平盘,此时
机械能增加量为动能增加量加上势能增加量和为
考查方向
解题思路
对物体受力分析可知,物理离开圆盘前,摩擦力和绳子的拉力提供圆周运动向心力,竖直方向受轻绳分力,支持力和重力作用。由几何关系可得圆周运动半径,由功能关系可知转台对物体做功,转台对物块支持力为零时,摩擦力为零则重力和拉力的合力提供圆周运动向心力,可得圆周运动速度进而知道动能。可求得转台对摩擦力做功。由角速度可知物体运动已经脱离圆盘,根据其圆周运动向心力的特点求解半径变化以及高度变化,进而求解变化的机械能
易错点
不能准确分析圆周运动过程的临界条件
知识点
4.北京时间2015 年12 月22 日9 时29 分,美国太空探索公司(SpaceX)成功发射新型火箭Falcon 9 FT,并在发射10 分钟后非常完美地回收了一级火箭,并成功将Orbcomm 公司的11 颗通讯卫星送入预定轨道。一级火箭的回收将大幅降低火箭发射费用,人类前往太空不再昂贵,廉价太空时代即将到来。如图为火箭通过尾部喷气正竖直向着降落平台减速降落的情景。火箭质量为m,喷出气体的质量相对于火箭质量很小,在离平台高h 时速度为v,降落过程中受空气的浮力和阻力大小之和为Ff,刚要落在平台上时的速度可忽略,降落过程中各力均可视为恒定。下列关于上述过程的描述正确的是( )
正确答案
解析
取火箭为研究对象,从高度为h的位置落回地面的过程,速度由v减为0,由动能定理有:
mgh-Ffh-Fh=0-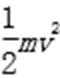
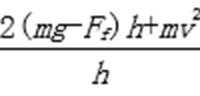
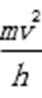
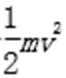
考查方向
解题思路
对火箭受力分析,分别写出牛顿第二定律和动能定理的方程求解。
易错点
① 机械能仅包括重力势能、弹性势能和动能;
② 加速度向上,物体处于超重状态,反之失重。
知识点
19.如图所示,斜面体B静置于水平桌面上,斜面上各处粗糙程度相同.一质量为M的木块A从斜面底端开始以初速度v0上滑,然后又返回出发点,此时速度为v,且v<v0,在上述过程中斜面体一直静止不动,以下说法正确的是
正确答案
解析
由于


A、当物体上滑时设斜面倾角为



B.当物体上滑时,物体B处于平衡状态,由平衡条件得:


C.由能理守恒定律可知,整个过程产生的热量为
D.由受力分析图可知物体上滑时,


考查方向
解题思路
对A进行受力分析,由滑动摩擦力公式判断A受到的滑动摩擦力如何变化;
对物体B受力分析,然后根据平衡条件分析答题。
易错点
受力分析是关键,对物体正确受力分析、熟练应用平衡条件列方程,解题时要注意受力分析的顺序,先对A受力分析,然后再对B受力分析。
知识点
16.如图,电梯质量为M,地板上放置一个质量为m的物体,轻质钢索拉电梯由静止开始向上加速运动,当上升高度为H时,速度达到v,不计空气阻力,则
正确答案
解析
A选项,对电梯与物体整体使用动能定理有:W拉力-(M+m)gH=


W支持力=
考查方向
1、考查动能定理的基本公式。
2、整体法与隔离法分析物体运动。
3、功率的公式P=Fv。
解题思路
1、对电梯与物体进行整体分析,受重力和绳子拉力,拉力做正功,重力做负功,写出动能定理的表达式:W拉力-(M+m)gH=
2、单独分析物体受重力和地板对物体的支持力,支持力做正功,重力做负功,写出动能定理的表达式:
W支持力-mgH=
3、根据功率公式P=Fv分析平均功率。
易错点
1、误认为绳子拉力做功等于物体动能变化量。
2、运用动能定理时对物体受力分析不完全。
3、不理解克服重力做功的含义:即重力做负功。
知识点
如图所示,长 L=0.20m 的不可伸长的轻绳上端固定在 O 点, 下端系一质量 m=0.10kg 的小球(可视为质点),将绳拉至水平位 置,无初速地释放小球。当小球运动至 O 点正下方的 M 点时,绳 刚好被拉断。经过一段时间,小球落到了水平地面上 P 点,P 点 与 M 点的水平距离 x=0.80m,不计空气阻力,取重力加速度 g=10m/s2。求:
23.小球运动至 M 点时的速率 v;
24.M 点距水平地面的高度 h。
25.绳所能承受的最大拉力 F 的大小;
正确答案
(1)2.0
解析
(1)小球自绳处于水平位置释放到最低点的过程机械能守恒,则有mgL=

考查方向
抛体运动功能关系、机械能守恒定律及其应用牛顿运动定律、牛顿定律的应用
解题思路
(1)因为是曲线运动,所以对小球由机械能守恒或者动能定理列方程求解;
易错点
不应该出错
正确答案
0.8m
解析
设小球自M点到P点的运动时间为t,则h=
考查方向
解题思路
由平抛运动规律求解。
易错点
不应该出错
正确答案
3N
解析
设小球通过最低点时绳的拉力为F′,根据牛顿第二定律有
考查方向
抛体运动功能关系、机械能守恒定律及其应用牛顿运动定律、牛顿定律的应用
解题思路
在M点由合力提供向心力可求F;
易错点
不应该出错
扫码查看完整答案与解析