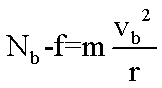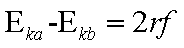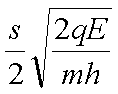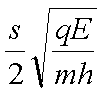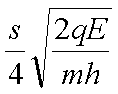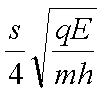- 带电粒子在匀强电场中的运动
- 共205题
为了降低潜艇噪音,提高其前进速度,可用电磁推进器替代螺旋桨。潜艇下方有左、右两组推进器,每组由6个相同的用绝缘材料制成的直线通道推进器构成,其原理示意图如下。在直线通道内充满电阻率ρ=0.2Ω∙m的海水,通道中a×b×c=0.3m×0.4m×0.3m的空间内,存在由超导线圈产生的匀强磁场,其磁感应强度B=6.4T、方向垂直通道侧面向外。磁场区域上、下方各有a×b=0.3m×0.4m的金属板M、N,当其与推进器专用直流电源相连后,在两板之间的海水中产生了从N到M,大小恒为I=1.0×103A的电流,设电流只存在于磁场区域。不计电源内阻及导线电阻,海水密度ρ≈1.0×103kg/m3。
(1)求一个直线通道推进器内磁场对通电海水的作用力大小,并判断其方向;
(2)在不改变潜艇结构的前提下,简述潜艇如何转弯?如何“倒车”?
(3)当潜艇以恒定速度v0=30m/s前进时,海水在出口处相对于推进器的速度v=34m/s,思考专用直流电源所提供的电功率如何分配,求出相应功率的大小。
正确答案
见解析。
解析
(1)安培力的大小,F=BIL=6.4×1000×0.3=1.92×103N,
根据左手定则可知,方向:垂直于BI平面向右;
(2)开启或关闭不同个数的左、右两侧的直线通道推进器,实施转弯。
改变电流方向,或改变磁场方向,可以改变海水所受磁场力的方向,实施“倒车”。
(3)电源提供的电功率中的第一部分为牵引功率
P1=F牵v0=6.9×105W
电源提供的电功率中的第二部分为单位时间内海水的焦耳热功率
推进器内海水的电阻
电源提供的电功率中的第三部分为单位时间内海水动能的增加量
单位时间内通过推进器的水的质量为
m=ρmbcv水对地=480kg
单位时间内其动能增加为P3=
知识点
如图甲所示,静电除尘装置中有一长为L、宽为b、高为d的矩形通道,其前、后面板使用绝缘材料,上、下面板使用金属材料。图乙是装置的截面图,上、下两板与电压恒定的高压直流电源相连。质量为m、电荷量为-q、分布均匀的尘埃以水平速度v0进入矩形通道,当带负电的尘埃碰到下板后其所带电荷被中和,同时被收集。通过调整两板间距d可以改变收集效率η。当d=d0时η为81%(即离下板081d0范围内的尘埃能够被收集)。不计尘埃的重力及尘埃之间的相互作用。
(1)求收集效率为100%时,两板间距的最大值dm;
(2)求收集率η与两板间距d的函数关系;
(3)若单位体积内的尘埃数为n,求稳定工作时单位时间下板收集的尘埃质量ΔM/Δt与两板间距d的函数关系,并绘出图线。
正确答案
见解析。
解析
(1)收集效率

在竖直方向有
其中 
当减少两板间距是,能够增大电场强度,提高装置对尘埃的收集效率。收集效率恰好为100%时,两板间距为
因此,在水平方向有
在竖直方向有 
其中
联立①②③④⑤⑥可得
(2)通过前面的求解可知,当

当 

根据题意,收集效率为 
联立①②③⑨⑩可得
(3)稳定工作时单位时间下板收集的尘埃质量
当 


绘出的图线如下:
知识点
如图,在第一象限存在匀强磁场,磁感应强度方向垂直于纸面(xy平面)向外;在第四象限存在匀强电场,方向沿x轴负向。在y轴正半轴上某点以与x轴正向平行、大小为

(1)电场强度大小与磁感应强度大小的比值;
(2)该粒子在电场中运动的时间。
正确答案
见解析。
解析
(1)如图,粒子进入磁场后做匀速圆周运动。设磁感应强度的大小为B,粒子质量与所带电荷量分别为m和q,圆周运动的半径为

由题给条件和几何关系可知
设电场强度大小为E,粒子进入电场后沿x轴负方向的加速度大小为




由于粒子在电场中做类平抛运动(如图),有

联立①②③④⑤⑥式得

(2)联立⑤⑥式得

(评分参考:第(1)问18分,①式3分,②式1分,③④⑤⑥式各3分,⑦式2分;第(2)问2分,⑧式2分)
知识点
如图,O.A.B为同一竖直平面内的三个点,OB沿竖直方向,

求:(1)无电场时,小球到达A点时的动能与初动能的比值;
(2)电场强度的大小和方向。
正确答案
见解析
解析
(1)设小球的初速度为





又有 
由①②③式得 
设小球到达A点时的动能为

由④⑤式得


(2)加电场后,小球从O点到A点和B点,高度分别降低了





在匀强电场中,沿任一直线,电势的降落是均匀的。设直线OB上的M点与A点等电势,M与O点的距离为x,如图,则有

解得x=d,MA为等势线,电场必与其垂线OC方向平行。设电场方向与竖直向下的方向的夹角为

即电场方向与竖直向下的方向的夹角为30°。
设场强的大小为E,有

由④⑦(11)式得 E=
知识点
注入工艺中,初速度可忽略的离子P+和P3+,经电压为U的电场加速后,垂直进入磁感应强度大小为B、方向垂直纸面向里,有一定的宽度的匀强磁场区域,如图所示,已知离子P+在磁场中转过=30°后从磁场右边界射出。在电场和磁场中运动时,离子P+和P3+
正确答案
解析
根据





知识点
匀强电场的方向沿x轴正向,电场强度E随x的分布如图所示。图中E0和d均为已知量。将带正电的质点A在O点由能止释放,A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放,当B在电场中运动时,A. B间的相互作用力及相互作用能均为零。B离开电场后,A、B间的相作用视为静电作用,已知A的电荷量为Q,A和B的质量分别为m和1/4m,不计重力。
(1)求A在电场中的运动时间t;
(2)若B的电荷量
(3)为使B离开电场后不改变运动方向.求B所带电荷量的最大位qm;
正确答案
见解析。
解析
(1)由牛顿第二定律,A在电场中运动的加速度a=
A在电场中做匀变速直线运动 d=
解得运动时间 t=
(2)设A、B离开电场时的速度分别为υA0、υB0,由动能定理,有
QE0d=


A、B相互作用过程中,动量和能量守恒。A、B相互作用力为斥力,A受的力与其运动方向相同,B受的力与其运动方向相反,相互作用力对A做正功,对B做负功。A、B靠近的过程中,B的路程大于A的路程,由于相互作用力大小相等,相互作用力对B做功的绝对值大于对A做功的绝对值,因此相互作用力做功之和为负,相互作用能增加。所以,当A、B最接近时相互作用能最大,此时两者速度相同,设为υ′,有
(m+

Epm=(




已知=
相互作用能的最大值 Epm=
(3)考虑A、B在x > d区间的运动,由动量守恒、能量守恒,且在初态和末态均无相互作用,有:
mυA+







由④、⑤解得 υB=-

因B不改变运动方向,故 υB=-

由①、⑥解得 q≤
即B所带电荷量的最大值 qm=
知识点
如图所示,水平放置的不带电的平行金属板p和h相距h,与图示电路相连,金属板厚度不计,忽略边缘效应。p板上表面光滑,涂有绝缘层,其上O点右侧相距h处有小孔K;b板上有小孔T,且O、T在同一条竖直线上,图示平面为竖直平面。质量为m、电荷量为- q(q > 0)的静止粒子被发射装置(图中未画出)从O点发射,沿P板上表面运动时间t后到达K孔,不与板碰撞地进入两板之间。粒子视为质点,在图示平面内运动,电荷量保持不变,不计空气阻力,重力加速度大小为g。
(1)求发射装置对粒子做的功;
(2) 电路中的直流电源内阻为r,开关S接“1”位置时,进入板间的粒子落在h板上的A点,A点与过K孔竖直线的距离为l。此后将开关S接“2”位置,求阻值为R的电阻中的电流强度;
(3) 若选用恰当直流电源,电路中开关S接“l”位置,使进入板间的粒子受力平衡,此时在板间某区域加上方向垂直于图面的、磁感应强度大小合适的匀强磁场(磁感应强度B只能在0~Bm=
正确答案
见解析
解析
解析:(1)设粒子在p板上做匀速直线运动的速度为v0,有
h=v0t ①
设发射装置对粒子做的功为W,由动能定律

联立①②式可得 
说明:①②式各2分,③式各1分
(2)S接“1”位置时,电源的电动势E0与板间电势差U有
E0=U ④
板间产生匀强电场的场强为E,粒子进入板间时有水平方向的速度v0,在板间受到竖直方向的重力和电场力作用而做累平抛运动,设加速度为a,运动时间为t1,有
U=Eh ⑤
mg-qE=ma ⑥

l=v0 t1 ⑧
S接“2”位置时,则在电阻R上流过的电流I满足

联立①④~⑨式得 
说明:④~⑩式各1分
(3)由题意知此时在板间运动的粒子重力与电场力平衡,当粒子从K进入板间后立即进入磁场做匀速圆周运动,如图所示,粒子从D点出磁场区域后沿DT做匀速直线运动,DT与b板上表面的夹角为题目所求夹角θ,磁场的磁感应强度B取最大值时的夹角θ为最大值θm,设粒子做匀速圆周运动的半径为R,有

过D点作b板的垂线与b板的上表面交于G,由几何关系有



联立①⑾~⒁式,将B=Bm代入,求得

当B逐渐减小,粒子做匀速圆周运动的半径为R也随之变大,D点向b板靠近,DT与b板上表面的夹角θ也越变越小,当D点无限接近于b板上表面时,粒子离开磁场后在板间几乎沿着b板上表面从T孔飞出板间区域,此时Bm>B>0满足题目要求,夹角θ趋近θ0,即
θ0=0 ⒃
则题目所求为 
知识点
离子推进器是太空飞行器常用的动力系统,某种推进器设计的简化原理如图1所示,截面半径为R的圆柱腔分为两个工作区。I为电离区,将氙气电离获得1价正离子II为加速区,长度为L,两端加有电压,形成轴向的匀强电场。I区产生的正离子以接近0的初速度进入II区,被加速后以速度vM从右侧喷出。
I区内有轴向的匀强磁场,磁感应强度大小为B,在离轴线R/2处的C点持续射出一定速度范围的电子。假设射出的电子仅在垂直于轴线的截面上运动,截面如图2所示(从左向右看)。电子的初速度方向与中心O点和C点的连线成α角(0<α<90◦)。推进器工作时,向I区注入稀薄的氙气。电子使氙气电离的最小速度为v0,电子在I区内不与器壁相碰且能到达的区域越大,电离效果越好。已知离子质量为M;电子质量为m,电量为e。(电子碰到器壁即被吸收,不考虑电子间的碰撞)。
(1)求II区的加速电压及离子的加速度大小;
(2)为取得好的电离效果,请判断I区中的磁场方向(按图2说明是“垂直纸面向里”或“垂直纸面向外”);
(3)ɑ为90◦时,要取得好的电离效果,求射出的电子速率v的范围;
(4)要取得好的电离效果,求射出的电子最大速率vM与α的关系。
正确答案
见解析
解析
解析:(1)由动能定理:
Ue=
解得 U=
由运动学公式v2=2aL
解得a=
(2)由右手定则磁场方向应垂直于纸面向外
(3)当α=900时,电子最大的圆直径为

据
所以
(4)做出临界轨迹圆与壁相切于B,圆心为A连接B、A、O,由几何知识知三者必然共线,
由余弦定理
据
故
知识点
如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行。a、b为轨道直径的两端,该直径与电场方向平行。一电荷为q(q>0)的质点沿轨道内侧运动.经过a点和b点时对轨道压力的大小分别为FNa和FNb不计重力,求电场强度的大小E、质点经过a点和b点时的动能。
正确答案
见解析
解析
解析:质点所受电场力的大小为f=qE,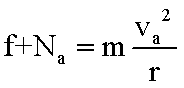
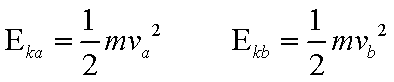
综上得: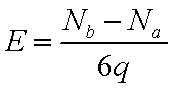
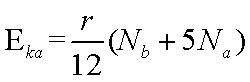
知识点
如图,场强大小为E.方向竖直向下的匀强电场中有一矩形区域abcd,水平边ab长为s,竖直边ad长为h。质量均为m.带电量分别为+q和-q的两粒子,由a.c两点先后沿ab和cd方向以速率v0进入矩形区(两粒子不同时出现在电场中)。不计重力。若两粒子轨迹恰好相切,则v0等于( )
正确答案
解析
略
知识点
扫码查看完整答案与解析