- 电磁学
- 共4057题
18．如图所示为某种质谱仪的工作原理示意图。此质谱仪由以下几部分构成：粒子源N；P、Q间的加速电场；静电分析器，即中心线半径为R的四分之一圆形通道，通道内有均匀辐射电场，方向沿径向指向圆心O，且与圆心O等距的各点电场强度大小相等；磁感应强度为B的有界匀强磁场，方向垂直纸面向外；胶片MO。由粒子源发出的不同带电粒子，经加速电场加速后进入静电分析器，某些粒子能沿中心线通过静电分析器并经小孔S垂直磁场边界进入磁场，最终打到胶片上的某点。粒子从粒子源发出时的初速度不计，粒子所受重力不计。下列说法中正确的是
A
B从小孔S进入磁场的粒子动能一定相等
C打到胶片上同一点的粒子速度大小不一定相等
D打到胶片上位置距离O点越远的粒子，比荷越小
正确答案
解析
粒子在直线加速过程，根据动能定理有：
电场中偏转过程，电场力提供向心力，根据牛顿第二定律有：
粒子在磁场中偏转过程，洛伦兹力提供向心力，根据牛顿第二定律有：
A、由方程①②解得：
由⑤式分析可知，只要满足
B、由①式分析可知从小孔S进入磁场的粒子动能为qU，故不同电量的粒子的动能不同，故B错误；
C、由③④联立解得：
D、由③④联立解得：
考查方向
带电粒子在匀强磁场中的运动
解题思路
带电粒子在电场中运动，电场力做正功，粒子做加速运动；后垂直于电场线，在电场力提供向心力作用下，做匀速圆周运动；最后进入匀强磁场，在洛伦兹力作用下，做匀速圆周运动；根据以上分析结合动能定理和牛顿第二定律列式解答.
易错点
本题关键是根据题意推导出带电粒子进入匀强磁场的半径公式与速度公式，据表达式分析解答.
知识点
公路工程施工监理招标，招标人选择中标人的基本原则是基于对投标人( )的选择。
A．经验多少
B．能力强弱
C．财务状况和社会信誉
D．报价高低
正确答案
B
解析
暂无解析
如图所示，在直角坐标系的第Ⅰ象限分布着场强E=5×103V/m、方向水平向左的匀强电场，其余三个象限分布着垂直纸面向里的匀强磁场．现从电场中M（0.5m，0.5m）点由静止释放一比荷为
28.匀强磁场的磁感应强度；
29.带电微粒第二次进入磁场时的位置坐标；
30.带电微粒第二次进入磁场时的速度大小和方向
正确答案
B=
解析
根据动能定理得
代入数据得：
因为微粒第一次进入磁场后将垂直通过x轴，
根据几何关系知，粒子在磁场中做圆周运动的半径
，
解得:
考查方向
带电粒子在复合场中的运动
解题思路
带电粒子在匀强电场中做的是类平抛运动，利用平抛运动规律，结合电场强度、电荷的荷质比，求出粒子的进入磁场的速度大小与方向以及位置．当带电粒子进入磁场后，仅受洛伦兹力作用，做匀速圆周运动．由微粒第一次进入磁场后将垂直通过x轴，可寻找到已知长度与圆弧半径的关系，从而求出磁感应强度
易错点
画出带电粒子的运动轨迹
正确答案
粒子垂直进入电场，做类平抛运动，
则a抛=
xM=
则y=vt抛=104×10﹣4=1m； （1分）
带电微粒第二次进入磁场时的位置坐标为（0m，1m） （1分）
解析
粒子垂直进入电场，做类平抛运动，
则a抛=
xM=
则y=vt抛=104×10﹣4=1m； （1分）
带电微粒第二次进入磁场时的位置坐标为（0m，1m） （1分）
考查方向
带电粒子在复合场中的运动
解题思路
带电粒子在匀强电场中做的是类平抛运动，利用平抛运动规律，结合电场强度、电荷的荷质比，求出粒子的进入磁场的速度大小与方向以及位置．当带电粒子进入磁场后，仅受洛伦兹力作用，做匀速圆周运动．由微粒第一次进入磁场后将垂直通过x轴，可寻找到已知长度与圆弧半径的关系，从而求出磁感应强度，当粒子再次进入电场时，仍是类平抛运动．利用相同方法求出离开电场的位置．
易错点
画出带电粒子的运动轨迹
正确答案
第二次进入磁场时：
Vx=a抛t抛=108×10﹣4=104m/s （1分）
V=
速度方向与Y轴夹角450 （1分）
解析
第二次进入磁场时：
Vx=a抛t抛=108×10﹣4=104m/s （1分）
V=
速度方向与Y轴夹角450 （1分）
考查方向
带电粒子在复合场中的运动
解题思路
带电粒子在匀强电场中做的是类平抛运动，利用平抛运动规律，结合电场强度、电荷的荷质比，求出粒子的进入磁场的速度大小与方向以及方向．
易错点
画出带电粒子的运动轨迹
如图甲所示，建立Oxy坐标系，两平行极板P、Q垂直于y轴且关于x轴对称，极板长度和板间距均为l，第一四象限有磁场，方向垂直于Oxy平面向里。位于极板左侧的粒子源沿x轴间右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子在0~3t0时间内两板间加上如图乙所示的电压（不考虑极边缘的影响）。
已知t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场。上述m、q、l、t0、B为已知量。（不考虑粒子间相互影响及返回板间的情况）
28.求电压U0的大小；
29.求
30.何时进入两板间的带电粒子在磁场中的运动时间最短？求此最短时间。
正确答案
见解析
解析
t=0时刻进入两极板的带电粒子在电场中做匀变速曲线运动，t0时刻刚好从极板边缘射出，在y轴负方向偏移的距离为l/2，则有
Eq=ma ②
l/2=at02/2 ③
联立以上①②③式，
解得: 
考查方向
解题思路
t=0时刻进入两极板的带电粒子在电场中做匀变速曲线运动，t0时刻刚好从极板边缘射出，在y轴负方向偏移的距离为l/2。t0/2时刻进入两极板的带电粒子，前t0/2时间在电场中偏转，后t0/2时间两极板没有电场，带电粒子做匀速直线运动
2t0时刻进入两极板的带电粒子在磁场中运动时间最短。
易错点
正确分析周期性变化的电场是解决本题的关键
正确答案
见解析
解析
t0/2时刻进入两极板的带电粒子，前t0/2时间在电场中偏转，后t0/2时间两极板没有电场，带电粒子做匀速直线运动。
带电粒子沿x轴方向的分速度大小为v0=l/t0 ⑤
带电粒子离开电场时沿y轴负方向的分速度大小为
带电粒子离开电场时的速度大小为
设带电粒子在磁场做匀速圆周运动半径为R，则有
联立③⑤⑥⑦⑧式解得
考查方向
解题思路
t=0时刻进入两极板的带电粒子在电场中做匀变速曲线运动，t0时刻刚好从极板边缘射出，在y轴负方向偏移的距离为l/2。t0/2时刻进入两极板的带电粒子，前t0/2时间在电场中偏转，后t0/2时间两极板没有电场，带电粒子做匀速直线运动
2t0时刻进入两极板的带电粒子在磁场中运动时间最短。
易错点
正确分析周期性变化的电场是解决本题的关键
正确答案
见解析
解析
2t0时刻进入两极板的带电粒子在磁场中运动时间最短。
带电粒子离开磁场时沿y轴正方向的分速度为
设带电粒子离开电场时速度方向与y轴正方向的夹角为
联立③⑤⑩式解得
磁场中运动周期
考查方向
解题思路
t=0时刻进入两极板的带电粒子在电场中做匀变速曲线运动，t0时刻刚好从极板边缘射出，在y轴负方向偏移的距离为l/2。t0/2时刻进入两极板的带电粒子，前t0/2时间在电场中偏转，后t0/2时间两极板没有电场，带电粒子做匀速直线运动
2t0时刻进入两极板的带电粒子在磁场中运动时间最短。
易错点
正确分析周期性变化的电场是解决本题的关键
下列有关收入确认的表述中，正确的有( )。
A．广告制作佣金应在相关广告或商业行为开始出现于公众面前时，确认为劳务收入
B．与商品销售收入分开的安装费，应在资产负债表日根据安装的完工程度确认为收入
C．对附有销售退回条件的商品销售，如不能合理地确定退货的可能性，则应在售出商品退货期满时确认收入
D．劳务开始和完成分属于不同的会计年度时，在劳务结果能够可靠估计的情况下，应在资产负债表日按完工百分比法确认收入
E．对附有销售退回条件的商品销售，必须在退货期满时才确认收入
正确答案
B,C,D
解析
[解析] 广告制作佣金应在资产负债表日根据项目完成的程度确认劳务收入；对附有销售退回条件的商品销售，企业能够合理估计退货的可能性且确认与退货相关的负债的，通常应在发出商品时确认收入。
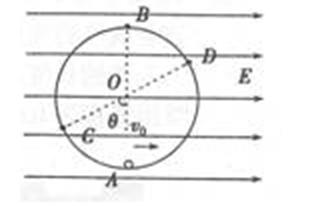
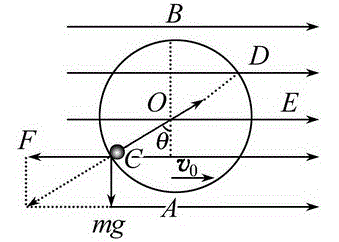
如图所示，在竖直平面内固定的圆形绝缘轨道的圆心在
O点，半径为r，内壁光滑，A、B两点分别是圆形轨道的最低点
和最高点．该区域存在方向水平向右的匀强电场，一质量为m、
带负电的小球在轨道内侧做完整的圆周运动（电荷量不变），经过
C点时速度最大，O、C连线与竖直方向的夹角θ=60°，重力加
速度为g．求：
26.小球受到的电场力的大小；
27.小球在A点的速度vo多大时，小球经过B点时对轨道的压力最小？
正确答案
F＝mg. （2分）
解析
小球经过C点时速度最大，则在该点电场力与重力的合力沿半径方向，小球受到的电场力的大小 F＝mgtan 60° （2分）
F＝mg. （2分）
考查方向
带电粒子在匀强电场中的运动
解题思路
抓住带电小球运动至C点的速度最大这一突破口，竖直面内圆周运动的最大速度出现在物理“最低点”，即合外力沿半径指向圆心，而电场力和重力的合力则背离圆心的方向
易错点
小球经C点时速度最大这也关键突破口展开讨论
正确答案
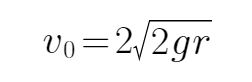
解析
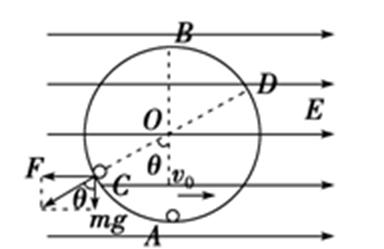
小球经过B点时对轨道的压力最小，则需小球到达D点时速度最小．设小球在D点时轨道对小球的压力恰好为零，
有
＝m （ 2分）
v＝ （ 2分）
在小球在轨道上由A点运动到D点的过程中有：
mg·r(1＋cos θ)＋F·rsin θ＝mv－mv2 （ 4分）
解得：v0＝2. （2分）
考查方向
带电粒子在匀强电场中的运动
解题思路
竖直面内圆周运动的最高点，轨道对小球的压力竖直向下，对B的压力最小时，对D的最小压力等于零．
易错点
小球在B点压力对轨道压力最小为0，根据指向圆心的合力提供圆周运动向心力为解题关键．
如图所示，M、N为中心开有小孔的平行板电容器的两极板，相距为D，其右侧有一边长为2a的正三角形区域，区域内有垂直纸面向里的匀强磁场，在极板M、N之间加上电压U后，M板电势高于N板电势．现有一带正电的粒子，质量为m，电荷量为q，其重力和初速度均忽略不计，粒子从极板M的中央小孔s1处射入电容器，穿过小孔s2后从距三角形A点
试求：
29.粒子到达小孔s2时的速度；
30.若粒子从P点进入磁场后经时间t从AP间离开磁场，求粒子的运动半径和磁感应强度的大小；
31．若粒子能从AC间离开磁场，磁感应强度应满足什么条件？
正确答案
解析
粒子在电场中运动时，根据动能定理，有：
解得：
考查方向
带电粒子在匀强电场中的运动
解题思路
粒子在加速电场中，电场力做功，由动能定理求出末速度v
易错点
基础题，不应该出错
教师点评
本题是带电粒子在组合场中运动的问题，粒子在磁场中做匀速圆周运动，要能画出粒子运动的轨迹，能根据半径公式，周期公式结合几何关系求解，难度适中．
正确答案
解析
粒子从进入磁场到从AP间离开：
解得：
由
解得：
考查方向
带电粒子在匀强磁场中的运动
解题思路
粒子从进入磁场到从AP间离开，轨迹为半圆周，根据半径公式，周期公式结合几何关系即可求解
易错点
对带电粒子在匀强磁场中运动的解决思路不熟悉
教师点评
本题是带电粒子在组合场中运动的问题，粒子在磁场中做匀速圆周运动，要能画出粒子运动的轨迹，能根据半径公式，周期公式结合几何关系求解，难度适中．
正确答案
解析
如图，粒子要能从AC间离开磁场的两条临界轨迹，由几何关系知：
由
所以 磁感应强度应满足什么条件
考查方向
带电粒子在匀强磁场中的运动
解题思路
粒子从进入磁场到从AP间离开，画出运动轨迹，找出临界状态，根据半径公式结合几何关系即可求解
易错点
找出临界状态，画出运动轨迹
教师点评
本题是带电粒子在组合场中运动的问题，粒子在磁场中做匀速圆周运动，要能画出粒子运动的轨迹，能根据半径公式，周期公式结合几何关系求解，难度适中．
如图所示，M、N为中心开有小孔的平行板电容器的两极板，相距为D，其右侧有一边长为2a的正三角形区域，区域内有垂直纸面向里的匀强磁场，在极板M、N之间加上电压U后，M板电势高于N板电势．现有一带正电的粒子，质量为m，电荷量为q，其重力和初速度均忽略不计，粒子从极板M的中央小孔s1处射入电容器，穿过小孔s2后从距三角形A点
16.粒子到达小孔s2时的速度；
17. 若粒子从P点进入磁场后经时间t从AP间离开磁场，求粒子的运动半径和磁感应强度的大小；
18.若粒子能从AC间离开磁场，磁感应强度应满足什么条件？
正确答案
(1)带电粒子在电场中运动时由动能定理得： 
解得粒子进入磁场时的速度大小为 
解析
(1)带电粒子在电场中运动时由动能定理得：
解得粒子进入磁场时的速度大小为
考查方向
带电粒子在匀强电场中加速
解题思路
粒子在加速电场中，电场力做功，由动能定理求出末速度v
易错点
基础题，不应该出错
正确答案
(2) 粒子的轨迹图如图甲所示，粒子从进入磁场到从AP间离开，
由牛顿第二定律得： 
粒子在磁场中运动的时间为 
由以上两式可解得轨道半径 
磁感应磁强度为 
解析
(2) 粒子的轨迹图如图甲所示，粒子从进入磁场到从AP间离开，
由牛顿第二定律得：
粒子在磁场中运动的时间为
由以上两式可解得轨道半径
磁感应磁强度为
考查方向
带电粒子在匀强磁场中的运动
解题思路
粒子从进入磁场到从AP间离开，根据半径公式，周期公式结合几何关系即可求解
易错点
画出粒子运动的轨迹
教师点评
本题是带电粒子在组合场中运动的问题，粒子在磁场中做匀速圆周运动，要能画出粒子运动的轨迹，能根据半径公式，周期公式结合几何关系求解，难度适中．
正确答案
（3）粒子从进入磁场到从AC间离开，若粒子恰能到达BC边界，如图乙所示，设此时的磁感应强度为B1，根据几何关系有此时粒子的轨道半径为 [来源:]
由牛顿第二定律可得
解得
粒子从进入磁场到从AC间离开，若粒子恰能到达AC边界，如图丙所示，设此时的磁感应强度为B2，
根据几何关系有：
由牛顿第二定律得 
由以上两式解得
综上所述要使粒子能从AC间离开磁场，磁感应强度应满足：
解析
（3）粒子从进入磁场到从AC间离开，若粒子恰能到达BC边界，如图乙所示，设此时的磁感应强度为B1，根据几何关系有此时粒子的轨道半径为
由牛顿第二定律可得
解得
粒子从进入磁场到从AC间离开，若粒子恰能到达AC边界，如图丙所示，设此时的磁感应强度为B2，
根据几何关系有：
由牛顿第二定律得
由以上两式解得
综上所述要使粒子能从AC间离开磁场，磁感应强度应满足：
考查方向
带电粒子在匀强磁场中的运动的临界条件
解题思路
粒子从进入磁场到从AC间离开，画出运动轨迹，找出临界状态，根据洛伦兹力提供向心力结合几何关系即可求解．
易错点
找出临界状态
教师点评
本题是带电粒子在组合场中运动的问题，粒子在磁场中做匀速圆周运动，要能画出粒子运动的轨迹，能根据半径公式，周期公式结合几何关系求解，难度适中．
如图所示，长L＝0.125 m、质量M＝30g的绝缘薄板置于倾角为θ=37°的斜面PM底端P， PN是垂直于PM的挡板，斜面与薄板间的动摩擦因数μ0＝0.8 .质量m＝10g、带电荷量q＝＋2.5×10-3C可视为质点的小物块放在薄板的最上端，薄板和物块间的动摩擦因数μ＝0.5，所在空间加有一个方向垂直于斜面向下的匀强电场E．现对薄板施加一平行于斜面向上的拉力F＝0.726N，当物块即将离开薄板时，立即将电场E方向改为竖直向上，同时增加一个垂直纸面向外B=6.0T足够大的匀强磁场，并撤去外力F，此时小物块刚好做匀速圆周运动. 设最大静摩擦力与滑动摩擦力相同，不考虑因空间电、磁场的改变而带来的其它影响，斜面和挡板PN均足够长．取g＝10 m/s2，sin37=0.6．求：
13.电场强度E的大小；
14.小物块从开始运动至脱离薄板所需要的时间；
15.物块第一次击中挡板PN的位置。
正确答案
(1)40N/C
解析
因物块能在竖直面内做匀速圆周运动，所以必有：
考查方向
考查带电物体在电场、磁场、重力场的复合场中的运动模型。
解题思路
根据“刚好做匀速圆周运动”得出：重力等于电场力
易错点
1、对“刚好做匀速圆周运动”的物体条件不清楚。2、对物体的运动轨迹分析不准确。3、在计算时间时，对运动学的公式选择不当。
正确答案
(2)0.5s
解析
分别对物块、薄板进行受力分析，写出牛顿第二运动定律的表达式，求出各自的加速度，根据加速度运用运动学的基本公式，及空间位置关系：
考查方向
考查带分析电物体在磁场中的匀速圆周运动轨迹及其基本公式计算。
解题思路
分别对物块、薄板进行受力分析，写出牛顿第二运动定律的表达式，求出各自的加速度，根据加速度运用运动学的基本公式，及空间位置关系：
易错点
1、对“刚好做匀速圆周运动”的物体条件不清楚。2、对物体的运动轨迹分析不准确。3、在计算时间时，对运动学的公式选择不当。
正确答案
(3) 距P点的距离为：1.87m
解析
物块即将离开薄板时，物块发生的位移：
考查方向
考查牛顿第二运动定律及运动学中的滑块滑板模型。考查带电物体在匀强电场中的受力计算。
解题思路
析物块所受洛伦兹力的方向，根据公式
易错点
1、对“刚好做匀速圆周运动”的物体条件不清楚。2、对物体的运动轨迹分析不准确。3、在计算时间时，对运动学的公式选择不当。
2．如图所示，平行板电容器PQ 两板加一恒定电源，Q 板上有两小孔A、B。一带电粒子从小孔A 以一定的初速度射入平行板P 和Q 之间的真空区域，经偏转后打在Q 板上如图所示的位置。在其它条件不变的情况下要使该粒子能从Q 板上的小孔B 射出，下列操作中可能实现的是（不计粒子重力）( )
正确答案
解析
粒子在电场中做类斜抛运动，若要使粒子能过通过B点，则x=
若先断开开关S,则两极板间的场强不会随着间距的变化而改变，所以粒子的轨迹不会发生改变，可以通过适当的下移Q板实现粒子通过B点，CD均错误。
考查方向
解题思路
由斜抛运动的规律：若初速度为v0，初速度与“水平”方向夹角为θ，则水平射程为：
x=v0cosθ·2
易错点
类斜抛运动的规律。
知识点
5.竖直平面内存在一正方形区域ABCD，边长为L，AC 为对角线，一带电粒子质量为m,电荷量为+q，重力不计，以水平初速度为v0从A 点射入正方形区域，可在ACD 区域内加竖直方向的匀强电场或垂直平面的匀强磁场，使得带电粒子能从C 点射出场区域，则下列说法正确的是( )
正确答案
解析
若在ACD区域加入竖直向下的匀强电场，且使粒子从C点穿出，则粒子做类平抛运动，设正方形边长为l，则有l=v0t，l=
若在ACD区域加入垂直纸面向外的匀强磁场，洛伦兹力提供粒子做匀速圆周运动的向心力，由几何关系可知，粒子做圆周运动的半径r=
考查方向
解题思路
加入竖直向下的匀强电场，结合类平抛运动规律判断；再加入匀强磁场，根据圆周运动规律判断。
易错点
类平抛运动的推论不熟
知识点
7．如图所示，匀强电场中有一个以O为圆心、半径为R的圆，电场方向与圆所在平面平行，A、O两点电势差为U，一带正电的粒子在该电场中运动，经A、B两点时速度方向沿圆的切线，速度大小均为v0，粒子重力不计（ ）
A粒子在A、B间是做圆周运动
B粒子从A到B的运动过程中，动能先增大后减小
C匀强电场的电场强度E＝
D圆周上电势最高的点与O点的电势差为
正确答案
解析
考查方向
解题思路
带正电粒子仅在电场力作用下，从A运动到B，由速度大小，得出粒子的动能，从而确定粒子的电势能大与小．由于匀强电场，则等势面是平行且等间距．根据曲线运动条件可从而确定电场力的方向，从而得出匀强电场的电场线方向．
易错点
紧扣动能相等作为解题突破口，由于仅在电场力作用下，所以得出两点的电势能大小关系．并利用等势面与电场线垂直的特性，从而推出电场线位置．再由曲线运动来确定电场力的方向．同时考查U=Ed中d的含义重要性．
知识点
8．如图所示，M、N为两块带等量异种电荷的平行金属板，两板间电压可取从零到某一最大值之间的各种数值．静止的带电粒子带电荷量为＋q，质量为m （不计重力），从点P经电场加速后，从小孔Q进入N板右侧的匀强磁场区域，磁感应强度大小为B，方向垂直于纸面向外，CD为磁场边界上的一绝缘板，它与N板的夹角为θ＝30°，孔Q到板的下端C的距离为L，当M、N两板间电压取最大值时，粒子恰垂直打在CD板上，则：（ ）
A两板间电压的最大值Um＝
BCD板上可能被粒子打中区域的长度S＝
C粒子在磁场中运动的最长时间tm＝
D能打到N板上的粒子的最大动能为
正确答案
解析
A、M、N两板间电压取最大值时，粒子恰垂直打在CD板上，
所以圆心在C点，CH=QC=L，故半径R1=L
B、打在QE间的粒子在磁场中运动的时间最长，均为半周期：
T=
所以tm=1/2T=
考查方向
易错点
运动轨迹画不出
知识点
15．如图，在xOy平面第一象限内有平行于y轴的匀强 电场和垂直于xOy平面的匀强磁场。一质量为m、带电量为＋q的小球从y轴上离坐标原点距离为L的A点处，以沿x正向的初速度v0进入第一象限，小球恰好做匀速圆周运动，并从x轴上距坐标原点L／2的C点离开磁场。求：
（1）匀强电场电场强度E的大小和方向；
（2）磁感应强度B的大小和方向；
（3）如果撤去磁场，并且将电场反向，带电小球仍以相同的初速度从A点进入第一象限，求带电小球到达x轴时的坐标．
正确答案
（1）、
（2）、
（3）、
解析
解：（1）由带电小球做匀速圆周运动知，mg=Eq
所以 
（2）带电小球做匀速圆周运动时，洛仑兹力提供向心力
qv0B =mv02/R
B=mv0/(qR )
由圆周运动轨迹分析得 (L－R)2+(
R=5L/8
代入得
(3)电场反向后竖直方向受力 Eq+mg=ma
a=2g
小球做类平抛运动
得
考查方向
解题思路
见解析
易错点
第(3)问，合力恒定并且垂直初速度，所以小球做类平抛运动。
知识点
20．如图所示，直角三角形ABC区域中存在一匀强磁场，比荷相同的两个粒子（不计重力）沿AB方向射入磁场，分别从AC边上的P、Q两点射出，则
正确答案
解析
如图，粒子在磁场中做圆周运动，分别从P点和Q点射出，由图知，粒子运动的半径RP＜RQ，又粒子在磁场中做圆周运动的半径
考查方向
解题思路
粒子在磁场中做圆周运动，根据题设条件作出粒子在磁场中运动的轨迹，根据轨迹分析粒子运动半径和周期的关系，从而分析得出结论。
易错点
根据题意，画了轨迹，分析要求解的各量的关系是解题的关键。
知识点
扫码查看完整答案与解析