- 电磁学
- 共4057题
如图所示,边长为的L的正方形区域abcd中存在匀强磁场,磁场方向垂直纸面向里。一带电粒子从ad边的中点M点以一定速度垂直于ad边射入磁场,仅在洛伦兹力的作用下,正好从ab边中点N点射出磁场。忽略粒子受到的重力,下列说法中正确的是
正确答案
解析
略
知识点
如图2所示,一带电粒子,从a点以垂直磁场方向的速度v进入磁感应强度为B的有界匀强磁场中,沿着acb半圆弧运动,从b点飞出磁场,已测得半圆弧的直径ab长度为L,则下列说法中正确的是
正确答案
解析
略
知识点
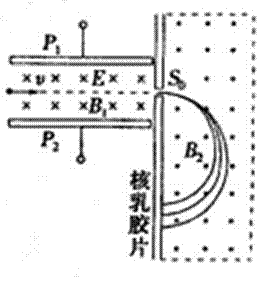
9.英国物理学家阿斯顿因首次制成质谱仪,并用此对同位素进行了研究,因此荣获了1922年的诺贝尔化学奖。若速度相同的同一束粒子由左端射入质谱仪后的运动轨迹如图所示,则下列相关说法中正确的是
正确答案
解析
略
知识点
如图所示,直角坐标系xoy位于竖直平面内,y轴正方向竖直向上,x轴正方向水平向右。空间中存在相互垂直的匀强电场和匀强磁场,匀强磁场垂直xoy平面向里,磁感应强度大小为B。匀强电场(图中未画出)方向平行于xoy平面,小球(可视为质点)的质量为m、带电量为+q,已知电场强度大小为
(1)若匀强电场方向水平向左,使小球在空间中做直线运动,求小球在空间中做直线运动的速度大小和方向;
(2)若匀强电场在xoy平面内的任意方向,确定小球在xoy平面内做直线运动的速度大小的范围;
(3)若匀强电场方向竖直向下,将小球从O点由静止释放,求小球运动过程中距x轴的最大距离。
正确答案
见解析。
解析
(1)由题意知小球做匀速直线运动
受力分析如图

匀速直线运动速度大小
方向如图,斜向下与x轴方向夹角45°
(2)小球做直线运动的条件为:洛仑兹力与电场力和重力的合力为一对平衡力。当电场在xoy平面内方向任意时,电场力与重力合力最大值为2mg
最小值为零
则:

得
(3)设小球运动到最低位置时下落高度为H,此时速度最大为v0,方向水平
任意时刻v沿x轴正向、y轴负向的分速度分别为vx,vy.。
与vy.对应的洛仑兹力水平分力方向沿x轴正向,
小球由静止释放到最低点的过程中,应用动量定理得:

小球由静止释放到最低点的过程中,由动能定理得:

解得
知识点
一种元素的两种同位素的原子核A和B,以相同速度垂直磁场方向射入同一匀强磁场中做匀速圆周运动。若认为中子和质子的质量是相同的,则它们的轨道半径之比等于
正确答案
解析
略
知识点
在竖直向上的匀强电场中,用细绳悬挂一个不带电的绝缘小球a,质量为m1。带电荷量为q、质量为m2的小球b以水平速度v与a相撞,如图所示。在a、b碰撞后的瞬间细绳断裂,并同时在该区域立即加上一个磁感应强度为B、垂直纸面向里的匀
强磁场,经过时间
正确答案
解析
略
知识点
24.如图所示,为一磁约束装置的原理图,圆心为原点



















(1)区域Ⅰ中磁感应强度
(2)若要使所有的粒子均约束在区域内,则环形区域Ⅱ中

(3)粒子从


正确答案
(1)
(3)
解析
(1)设在区域Ⅰ内轨迹圆半径为


∴
(2)设粒子在区域Ⅱ中的轨迹圆半径为
迹如图,有几何关系知:
方向与

由几何关系得
即
(3)轨迹从A点到Q点对应圆心角


其中
代入数据得:
知识点
25.如图14所示,在xOy平面内,以O′(0,R)为圆心、R为半径的圆内有垂直平面向外的匀强磁场,x轴下方有垂直平面向里的匀强磁场,两区域磁感应强度大小相等.第四象限有一与x轴成45°角倾斜放置的挡板PQ,P、Q两点在坐标轴上,且O、P两点间的距离大于2R,在圆形磁场的左侧0<y<2R的区间内,均匀分布着质量为m、电荷量为+q的一簇带电粒子,当所有粒子均沿x轴正向以速度v射入圆形磁场区域时,粒子偏转后都从O点进入x轴下方磁场,结果有一半粒子能打在挡板上。不计粒子重力、不考虑粒子间相互作用力。
求:
(1)磁场的磁感应强度B的大小;
(2)挡板端点P的坐标;
(3)挡板上被粒子打中的区域长度.
正确答案
见解析。
解析
(1)设一粒子自磁场边界A点进入磁场,该粒子由O点射出圆形磁场,轨迹如图甲所示,过A点做速度的垂线,长度为r,C为该轨迹圆的圆心.
连接AO′、CO,可证得ACOO′为菱形,根据图中几何关系可知:粒子在圆形磁场中的轨道半径r=R,
由qvB=
得B=
(2)有一半粒子打到挡板上需满足从O点射出的沿x轴负方向的粒子、沿y轴负方向的粒子轨迹刚好与挡板相切,如图乙所示,过圆心D作挡板的垂线交于E点,
DP=

P点的坐标为[(
(3)设打到挡板最左侧的粒子打在挡板上的F点,如图丙所示,OF=2R
过O点作挡板的垂线交于G点,
OG=(



EG=
挡板上被粒子打中的区域长度
知识点
如图所示,三个同心圆是磁场的理想边界,圆1半径R1=R、圆2半径R2=3R、圆3半径R3(R3>R2)大小未定,圆1内部区域磁感应强度为B,圆1与圆2之间的环形区域是无场区,圆2与圆3之间的环形区域磁感应强度也为B。两个区域磁场方向均垂直于纸面向里。t=0时一个质量为m,带电量为+q(q>0)的离子(不计重力),从圆1上的A点沿半径方向以速度 飞进圆1内部磁场。问:
(1)离子经多长时间第一次飞出圆1?
(2)离子飞不出环形磁场圆3边界,则圆3半径R3至少为多大?
(3)在满足了(2)小题的条件后,离子自A点射出后会在两个磁场不断地飞进飞出,从t=0开始到离子第二次回到A点,离子运动的总时间为多少?
(4)在同样满足了(2)小题的条件后,若环形磁场方向为垂直于纸面向外,其它条件不变,从t=0开始到离子第一次回到A点,离子运动的路径总长为多少?
正确答案
(1)
(2)
(3)
(4)
解析
(1)由 
根据几何知识:
离子在圆1中运动圆弧对应的圆心角为60°
得:
(2)依题意离子在环形磁场轨迹与圆3相切时对应的就是半径最小值,如图2:
由于两磁场的磁感应强度相同,有:
由图中几何关系得:
得:
(3)根据几何知识:
离子在圆2和圆3之间的运动圆弧对应的圆心角为240°
得: 
(只画了重复单程,这样的单程重复总共需6次)
从t=0开始到离子第二次回到A点,离子在圆1内磁场中运动共6次;
离子在环形磁场中运动共6次;离子在无场区中直线运动共12次。
在无场区离子直线单程的时间
总时间
(4)在原图中作图可知如下图:
(只画了重复单程,这样的单程重复总共需2次)
从t=0开始到离子第一次回到A点,离子在圆1内磁场中运动共2次;
离子在环形磁场中运动共2次;离子在无场区中直线运动共4次。
路径总长
知识点
14.如图甲所示,在y≥0的区域内有一个垂直纸面方向的有界匀强磁场,MN为磁场区域的上边界,磁场在x轴方向范围足够大。磁感应强度的变化如图乙所示,取垂直纸面向里为正方向。现有一带负电的粒子,质量为




求:(1)粒子在磁场中做圆周运动的半径和周期;
(2)若

(3)若
(4)若
正确答案
见解析。
解析
(1)由
得:
(2))粒子在t0=0s时刻进入磁场,在t=1×10-3s时,粒子

(3)粒子在t0=0s时刻进入磁场,粒子运动轨迹如图所示,要粒子垂直于MN离开磁场,可能从A、B等位置离开磁场
则磁场上边界MN与x轴间的距离:

(4)由图乙可知:磁场的变化周期


粒子在a、b、c等位置离开磁场时速度方向与它在O点的速度方向相同
若粒子在a、c等位置离开磁场,粒子在磁场中运动时间为:

若粒子在b等位置离开磁场,粒子在磁场中运动时间为:

综上所述:若t0=0.75×10-3s,粒子离开磁场时速度方向与它在O点的速度方向相同,则粒子通过磁场区域的时间

知识点
26.如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右边有一很薄的挡板,挡板与



(1)若在




(2)若在整个空间加一方向垂直纸面向里的匀强磁场,要使板右侧的MN连线上都有粒子打到,磁场的磁感应强度不能超过多少(用



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.如图所示,在垂直




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如右图所示,带有正电荷的A粒子和B粒子同时以同样大小的速度从宽度为d的有界匀强磁场的边界上的O点分别以30°和60°(与边界的夹角)射入磁场,又恰好都不从另一边界飞出,则下列说法中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.空间中有一直角坐标系,戈轴保持水平、方向向右,如图所示,在整个坐标空间有大小为B= 0.lT、方向垂直纸面向外的匀强磁场,在此坐标系第四象限内同时存在着水平方向的匀强电场E,一荷质比

(1)第四象限坐标中电场强度的大小和方向;
(2)带电微粒的运动速度;
(3)画出粒子运动轨迹图,并求出粒子离开第一象限的位置坐标。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24.用一根长L=0.8 m的轻绳,吊一质

(1)小球带何种电荷?电量为多少?
(2)当小球第二次经过最低点时,悬线23对小球的拉力多大?
正确答案
(1)设小球第一次到达最低点速度为V,则由动能定理可得:
在最低点由圆周运动规律得;
解得
(2)小球第二次到达最低点速度仍为V,
由圆周运动规律的:
解得F=0.06N
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析