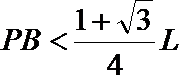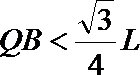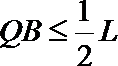- 电磁学
- 共4057题
26.如图所示,在光滑绝缘水平面上平放着一内壁光滑、绝缘的空心细管,管内M端有一带正电的小球P,在距离管的N端正右方2h的A1处有另一不带电的小球Q,存足够大空间区域有竖直向下的匀强磁场,磁感强皮为B。现让细管以垂直管长方向的速度v1水平向右匀速运动,同时让Q以某速度v2从A1点出发沿A1A2匀速运动,细管运动到A1处时,A1A2与细管延长线的夹角为45°。若小球P恰好在A处相对水平面以速度
(1)P的带电量与质量之比
(2)v2的人小。
正确答案
(1)设P的电量为q、质量为m,P因参与v1运动而受到指向N端的洛伦兹力,其值为
P在管中的运动会使它受到另一个向左的洛伦兹力,此力被管壁施予P向右的力所抵消。P对应有指向N端的加速度

设P从M端到达N端t1,到达N端时沿管长方向的速度大小为u。
则


由③可得:
由①②③⑤可得:
(2)P离开管后将在水平面上作匀速圆周运动其速度为:


P恰好在A1位置离开管的N端,离开管后最终只可能与Q在图中S处相碰,Q从开始运动到P相碰撞经历的时间为:

在这段时间内Q小球恰好走过2r的路程,则

解得:
解析
解析已在路上飞奔,马上就到!
知识点
22.如图甲所示,M、N为竖直放置的两块平行金属板,圆形虚线为与N相连且接地的圆形金属网罩(不计电阻)。PQ为与圆形网罩同心的金属收集屏,通过阻值为r0的电阻与大地相连。小孔s1、s2、圆心O与PQ中点位于同一水平线上。圆心角2θ=120°、半径为R的网罩内有大小为B,方向垂直纸面向里的匀强磁场。M、N间相距





(1)若质子在t >T时刻进入s1,为使质子能打到收集屏的中心需在圆形磁场区域加上一个匀强电场,求所加匀强电场的大小和方向?
(2)质子在哪些时间段内自s1处进入板间,穿出磁场后均能打到收集屏PQ上?
(3)若毎秒钟进入s1的质子数为n,则收集屏PQ电势稳定后的发热功率为多少?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图所示,匀强磁场的边界为直角三角形abc,一束相同的带负电的粒子以不同的速度v沿bc方向从b点射入磁场,不计粒子的重力,关于粒子在磁场中的运动情况下列说法正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 如图所示,在半径为R的圆形区域内,有匀强磁场,方向垂直于圆平面(未画出)。一群相同的带电粒子以相同速率


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.(18分)如下图,在


⑴ 求粒子在磁场中做圆周运动的速率v0
⑵ 假设粒子源在t=0时刻发射的上述粒子在0~180°范围内均匀分布,求


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.如图甲所示,直角坐标系中直线AB与横轴x夹角∠BAO=45°,AO长为a。假设在点A处有一粒子源可沿∠BAO所夹范围内的各个方向放射出质量为m、速度大小均为
(1)从顶点A沿AB方向射入的电子在磁场中的运动时间 t;
(2)磁场大小方向保持不变,改变匀强磁场分布区域,使磁场存在于三角形ABO内的
左侧,要使得电子从A点出发马上进入磁场且穿过有界磁场后都垂直y轴后向右运动,试求匀强磁场区域分布的最小面积;

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.如图所示,s为一电子发射枪,可以连续发射电子束,发射出来的电子初速度可视为0,电子经过平行板A、B之间的加速电场加速后,从o点沿x轴正方向进入xoy平面内,在第一象限内沿x、y轴各放一块平面荧光屏,两屏的交点为o,已知在y>0、0<x<a的范围内有垂直纸面向外的匀强磁场,在y>0、x>a的区域有垂直纸面向里的匀强磁场,大小均为B。已知给平行板AB提供直流电压的电源E可以给平行板AB提供0~U之间的各类数值的电压,现调节电源E的输出电压,从0调到最大值的过程中发现当AB间的电压为
(1)当电源输出电压调至
(2)两荧光屏上的发光亮线的范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
26.如图所示,一带电微粒质量为m=2.0×10-11kg、电荷量q=+1.0×10-5C,从静止开始经电压为U1=100V的电场加速后,水平进入两平行金属板间的偏转电场中,微粒射出电场时的偏转角θ=30º,并接着进入一个方向垂直纸面向里、宽度为D=34.6cm的匀强磁场区域。已知偏转电场中金属板长L=20cm,两板间距d=17.3cm,重力忽略不计。求:
(1)带电微粒进入偏转电场时的速率V1;
(2)偏转电场中两金属板间的电压U2;
(3)为使带电微粒不会由磁场右边射出,该匀强磁场的磁感应强度B至少多大?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如下图一所示,边界OA与OC之间分布有垂直纸面向里的匀强磁场,
边界OA上有一粒子源S。某一时刻,从|s平行于纸面向各个方向
发射出大量带正电的同种粒子(不计粒子的重力及粒子间的相互
作用),所有粒子的初速度大小相同,经过一段时间有大量粒子从
边界OC射出磁场。已知∠AOC =60°,从边界OC射出的粒子
在磁场中运动的最短时间等于
则从边界OC射出的粒子在磁场中运动的最长时间为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点

发射速率均为v、与y轴所成夹角θ可在0~1800范围
内变化的带负电的粒子。已知θ =450时,粒子恰好从磁
场右边界与P点等高的Q点射出磁场,不计重力及粒子间的相互作用。求
(1)磁场的磁感应强度;
(2)若θ=300,粒子射出磁场时与磁场边界的夹角
(可用三角函数、根式表示);
(3)能够从磁场右边界射出的粒子在磁场中经过的
区域的面积(可用根式表示)。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图所示,匀强磁场的边界为平行四边形ABDC,其中AC边与对角线BC垂直,一束电子以大小不同的速度沿BC从B点射入磁场,不计电子的重力和电子之间的相互作用,关于电子在磁场中运动的情况,下列说法中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 如图所示,有一垂直于纸面向外的有界匀强磁场,磁感应强度为B,其边界为一边长为 L的正三角形,A、B、C为三角形的三个顶点.若一质量为m、电荷量为+q的粒子(不计重力),以速度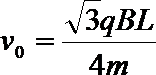
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 如图所示,两个电荷量分别为+q和-q的带电粒子分别以速度va和vb射入匀强磁场,两粒子的入射方向与竖直磁场边界的夹角分别为30°和60°,磁场宽度为d,两粒子同时由A点出发,同时到达与A等高的B点,如图所示,则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
25.如图所示,在xoy坐标的第I象限内存在垂直纸面向外的匀强磁场,磁感应强度为B,在x>0轴上有一平面荧光屏,在y轴上距坐标原点O为L的S处有一粒子源,在某时刻同时发射大量质量为m,电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~180°范围内.观察发现:荧光屏OP之间发光,P点右侧任何位置均无发光,在P、Q之间的任一位置会先后二次发光;O、Q之间的任一位置只有一次发光,测出O、P间距为
(1)粒子发射时的速度大小;

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形。已知带电粒子的质量为m,带电量为q,速度为υ,MN的长度为L,不计粒子重力
(1)若在y轴右侧加一平行于x轴的匀强电场,要使y轴右侧所有运动的粒子都能打到挡板MN上,则电场强度的最小值E0为多大?在电场强度为E0时,打到板上的粒子动能为多大?
(2)若在整个空间加一方向垂直纸面向里的匀强磁场,要使板的右侧在MN连线上都有粒子打到,磁场的磁感应强度不能超过多少(用m、υ、q、L表示)?
(3)若满足上述(2)的条件,放射源O向外发射出的所有带电粒子中有几分之几能打在板的右侧?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析