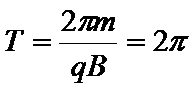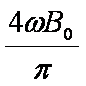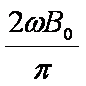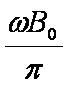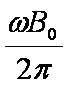- 电磁学
- 共4057题
如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.5 m,左端接有阻值R=0.3 Ω的电阻,一质量m=0.1 kg,电阻r=0.1 Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=0.4 T,棒在水平向右的外力作用下,由静止开始以a=2 m/s2的加速度做匀加速运动,当棒的位移x=9 m时撤去外力,棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比Q1∶Q2=2∶1,导轨足够长且电阻不计,棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触,求
(1)棒在匀加速运动过程中,通过电阻R的电荷量q;
(2)撤去外力后回路中产生的焦耳热Q2;
(3)外力做的功WF。
正确答案
(1)4.5 C
(2)1.8 J
(3)5.4 J
解析
(1)设棒匀加速运动的时间为



其中
设回路中的平均电流为

则通过电阻R的电荷量为
联立①②③④式,代入数据得q=4.5 C⑤
(2)设撤去外力时棒的速度为v,对棒的匀加速运动过程,由运动学公式得v2=2ax⑥
设棒在撤去外力后的运动过程中安培力做功为W,由动能定理得W=0-
撤去外力后回路中产生的焦耳热
Q2=-W⑧
联立⑥⑦⑧式,代入数据得
Q2=1.8 J⑨
(3)由题意知,撤去外力前后回路中产生的焦耳热之比Q1∶Q2=2∶1,可得Q1=3.6 J⑩
在棒运动的整个过程中,由功能关系可知WF=Q1+Q2⑪
由⑨⑩⑪式得WF=5.4 J。
知识点
如图所示,正方形区域MNPQ内有垂直纸面向里的匀强磁场,在外力作用下,一正方形闭合刚性导线框沿QN方向匀速运动,t=0时刻,其四个顶点M′、N′、P′、Q′恰好在磁场边界中点,下列图象中能反映线框所受安培力f的大小随时间t变化规律的是( )
正确答案
解析
第一段时间从初位置到M′N′离开磁场,图甲表示该过程的任意一个位置,切割磁感线的有效长度为M1A与N1B之和,即为M1M′长度的2倍,此时电动势E=2Bvtv,线框受的安培力

知识点
如图所示,在真空中,沿水平方向和竖起方向建立直角坐标系xOy,在x轴上方有一沿x轴正方向的匀强电场E(电场强度E的大小未知)。有一质量为m,带电量为+q的小球,从坐标原点O由静止开始自由下落,当小球运动到P(0,-h)点时,在x轴下方突然加一竖直向上的匀强电场,其电场强度与x轴上方的电场强度大小相等,且小球从P返回到O点与从O点下落到P点所用的时间相等。重力加速度为g。试求:
27.小球返回O点时速度的大小;
28.匀强电场的电场强度E的大小;
29.小球运动到最高点时的位置坐标。
正确答案
解析
设小球从O点运动到P点所用时间为t,在P点的速度为v1,返回O点时的速度为v2,则





考查方向
考查带电物体在电场中的运动:这类问题电场只是提供了一个电场力,可以转化为动力学问题求解,联系公式:
解题思路
首先分析小球从O点下落到P点再到O点的运动类型,明确这是两个阶段,应该分开分析,根据时间相等,及位移相等,解得小球回到O点时的速度。
易错点
在做运动学问题时,对公式的选择模糊不清,导致浪费时间,甚至解答困难。
正确答案
解析
(2)


考查方向
解题思路
根据运动学的基本公式解得小球在电场作用下的加速度a,再根据qE-mg=ma,解得E的大小。
易错点
在做运动学问题时,对公式的选择模糊不清,导致浪费时间,甚至解答困难。
正确答案
位置坐标为(4h,16h)
解析
在竖直方向:



考查方向
解题思路
小球进入x轴上方时,将小球的运动分解成竖直方向和水平方向,小球在竖直方向上做减速度为g的减速运动,在水平方向上在电场力作用下做匀加速运动,分别根据运动学公式计算两个方向的位移,得出小球的最高位置坐标。
易错点
在做运动学问题时,对公式的选择模糊不清,导致浪费时间,甚至解答困难。
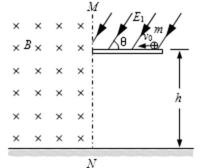
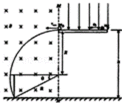
如图所示,水平地面上方竖直边界MN左侧存在垂直纸面向里的匀强磁场B和沿竖直方向的匀强电场E2(未画出),磁感应强度B=1.0 T,MN边界右侧离地面h= 3m处有长为L=0.91 m的光滑水平绝缘平台,平台的左边缘与MN重合,平台右边缘有一质量m=0.l kg、电量q=0.1C的带正电小球,以初速度v0=0.6m/s向左运动。此时平台上方存在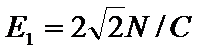
18.电场强度E2的大小和方向。
19.小球离开平台左侧后在磁场中运动的最短时间。
20.小球离开平台左侧后,小球落地点的范围。
正确答案
(1)电场强度E2的大小为10N/C,方向:竖直向上;
解析
(1)因为小球做匀速圆周运动,电场力必等于重力
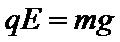
将数据代入①式解得: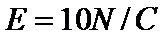
电场的方向竖直向上
考查方向
解题思路
(1)小球做匀速圆周运动,电场力等于重力,据此求出场强.
易错点
本题是小球在重力场、电场与磁场的复合场中运动类型,考查受力平衡的状态方程,机械能守恒与动量守恒定律的应用,关键要把握每个过程遵守的物理规律,结合几何知识进行处理.
正确答案
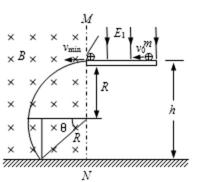
(2)小球离开平台左侧后在磁场中运动的最短时间为0.21s;
解析
(2)若θ=90°,小球匀速通过MN后有最小速度: 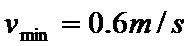
若θ=45°,小球匀速通过MN后有最大速度,由加速度公式可得:
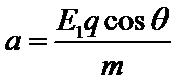
由匀变速直线运动规律可得: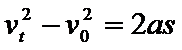
将数据代入④⑤式,可解得: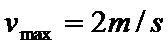
小球在通过MN的速度为大于等于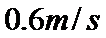
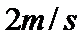
小球以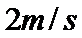
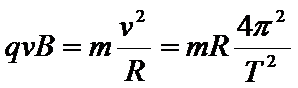
由⑦式可得: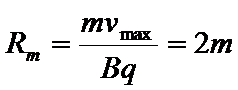
由⑦式解得:
因为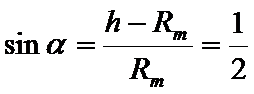
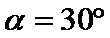
考查方向
解题思路
(2)小球在磁场中做匀速圆周运动,求出小球做圆周运动的圆心角,然后求出其运动时间.
易错点
本题是小球在重力场、电场与磁场的复合场中运动类型,考查受力平衡的状态方程,机械能守恒与动量守恒定律的应用,关键要把握每个过程遵守的物理规律,结合几何知识进行处理.
正确答案
(3)小球离开平台左侧后,小球落地点的范围是:在N点左边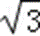
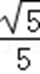
解析
(3)小球落在N点左边的最大距离时,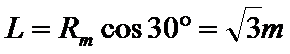
当小球落在右边最大距离时其对应在磁场中的轨道半径为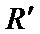
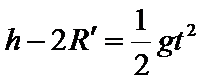
水平位移为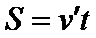
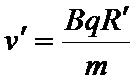
因此得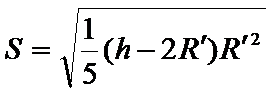
当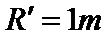
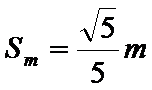
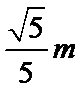
所以,小球的落点在距N点左边1.73m、右边0.447m的范围内
考查方向
解题思路
(3)求出小球落地点最左侧距离,然后求出落地点的右侧距离,然后确定其落地点范围.
易错点
本题是小球在重力场、电场与磁场的复合场中运动类型,考查受力平衡的状态方程,机械能守恒与动量守恒定律的应用,关键要把握每个过程遵守的物理规律,结合几何知识进行处理.
如图,在真空中竖直平面内同时存在多层厚度为d,足够宽的正交复合场,匀强电场的电场强度大小为



29.求小球在第1层复合场区域做圆周运动的轨道半径
30.求小球到达第2个复合场区域时速度方向与竖直方向夹角的正弦值;
31.若空间存在有n层复合场,小球不能从复合场下边界穿出,求n的最小值。
正确答案

解析
小球进入第1层复合场时,只有重力做功,由动能定理得:
在复合场中小球受重力与电场力相等,洛仑兹力提供圆周运动向心力,有:
联立解得:
考查方向
动能定理;带电粒子在匀强磁场中的运动
解题思路
由动能定理先求粒子进入第一层复合场的速度,进入复合场后,带电粒子在洛伦兹力提供向心力下在磁场中做匀速圆周运动.
易错点
本题关键要分析出当粒子进入复合场时,粒子做匀速圆周运动.
正确答案

解析
设从第1层复合场穿出时速度与竖直方向夹角为



设从第2层复合场进入时速度与竖直方向夹角为
根据动能定理
联立解得 :
考查方向
动能定理;带电粒子在匀强磁场中的运动
解题思路
由几何关系表示出从第1层复合场穿出时速度与竖直方向夹角,同理根据动能定理求出进入第1层复合场时速度的大小,在由几何关系表示出粒子进入第2层复合场时速度与竖直方向夹角,找两个角之间的关系;
易错点
本题关键是做出粒子的运动轨迹示意图,由几何关系求解.
正确答案

解析
设从第n层复合场进入时速度与竖直方向夹角为


小球在重力场中运动时,垂直于重力方向的速度分量不变,则:
联立得: 


根据动能定理


联立解得
考查方向
动能定理;带电粒子在匀强磁场中的运动
解题思路
根据几何关系找出从第n层复合场进入时的半径与d之间的关系,根据动能定理与牛顿第二定律求解.
易错点
进入第n层时粒子做匀速圆周运动的半径与d之间的关系是解决问题的关键.
容器A中装有大量的质量、电量不同但均带正电的粒子,粒子从容器下方的小孔 Sl不断飘人加速电场(初速度可视为零)做直线运动通过小孔S2后,从两平行板中央垂直电场方向射人偏转电场。粒子通过平行板后垂直磁场方向进入磁感应强度为B,方向垂直向里的匀强磁场区域,最后打在感光片上,如图所示。已知加速场S1、S2间的加速电压为 u,偏转电场极板长为L,两板间距也为L,板间匀强电场强度E=

26.粒子射入磁场时,其速度方向与边界ab间的夹角;
27.射到感光片Q处的粒子的比荷(电荷量与质量之比);
28.粒子在磁场中运动的最短时间。
正确答案
(1)
解析
(1)设质量为m,电量为q的粒子通过孔S2的速度为v0

粒子在平行板间:


联解①②③④得:
其速度方向与边界ab间的夹角
考查方向
解题思路
根据动能定理求出粒子经加速电场时的速度,粒子在偏转电场中做类平抛运动,求出其速度方向与边界ab间的夹角,由带电粒子在匀强磁场中的圆周运动确定出半径,然后求出射到感光片Q处的粒子的比荷,由粒子在磁场中运动的偏转角,求出粒子在磁场中运动的最短时间。
易错点
粒子射入磁场时的速度应为合速度,由几何关系确定粒子的运动半径大小,粒子在磁场中运动的偏转角的求解问题。
正确答案
(2)
解析
粒子从e板下端与水平方向成450的角射入匀强磁场。
设质量为m。
电量为q的粒子射入磁场时的速度为v,
做圆周运动的轨道半径为r

由可知:


联解⑤⑥⑦得:
粒子的比荷为:
考查方向
解题思路
根据动能定理求出粒子经加速电场时的速度,粒子在偏转电场中做类平抛运动,求出其速度方向与边界ab间的夹角,由带电粒子在匀强磁场中的圆周运动确定出半径,然后求出射到感光片Q处的粒子的比荷,由粒子在磁场中运动的偏转角,求出粒子在磁场中运动的最短时间。
易错点
粒子射入磁场时的速度应为合速度,由几何关系确定粒子的运动半径大小,粒子在磁场中运动的偏转角的求解问题。
正确答案
(3)
解析
设粒子在磁场中运动的时间为t


联解⑧⑨得:
因为所有粒子在磁场中运动的偏转角
所以粒子打在P处时间最短由几何知:r2+r2=L2 
联解⑩⑪得
粒子在磁场中的最短时间
考查方向
解题思路
根据动能定理求出粒子经加速电场时的速度,粒子在偏转电场中做类平抛运动,求出其速度方向与边界ab间的夹角,由带电粒子在匀强磁场中的圆周运动确定出半径,然后求出射到感光片Q处的粒子的比荷,由粒子在磁场中运动的偏转角,求出粒子在磁场中运动的最短时间。
易错点
粒子射入磁场时的速度应为合速度,由几何关系确定粒子的运动半径大小,粒子在磁场中运动的偏转角的求解问题。
如图,两根足够长的金属导轨ab、cd竖直放置,导轨间距离为L,电阻不计。在导轨上端并接两个额定功率均为P、电阻均为R的小灯泡。整个系统置于匀强磁场中,磁感应强度方向与导轨所在平面垂直。现将一质量为m、电阻可以忽略的金属棒MN从图示位置由静止开始释放。金属棒下落过程中保持水平,
(1)磁感应强度的大小;
(2)灯泡正常发光时导体棒的运动速率。
正确答案
(1)设小灯泡的额定电流I0,有:P=I02R①
由题意,在金属棒沿着导轨竖直下落的某时刻后,小灯泡保持正常发光,流经MN的电流为 I=2I0②
此时刻金属棒MN所受的重力和安培力相等,下落的速度达到最大值,有 mg=BLI③
联立①②③式得 
(2)设灯泡正常发光时,导体棒的速率为v,由电磁感应定律与欧姆定律得
E=BLv⑤
E=RI0⑥
联立①②④⑤⑥式得 v=
解析
略。
知识点
如图,一载流长直导线和一矩形导线框固定在同一平面内,线框在长直导线右侧,且其长边与长直导线平行。已知在t=0到t=t1的时间间隔内,直导线中电流i发生某种变化,而线框中感应电流总是沿顺时针方向;线框受到的安培力的合力先水平向左、后水平向右。设电流i正方向与图中箭头方向相同,则i随时间t变化的图线可能是
正确答案
解析
要求框中感应电流顺时针,根据楞次定律,可知框内磁场要么向里减弱(载流直导线中电流正向减小),要么向外增强(载流直导线中电流负向增大)。线框受安培力向左时,载流直导线电流一定在减小,线框受安培力向右时,载流直导线中电流一定在增大。故答案选A。
知识点
如图,均匀磁场中有一由半圆弧及其直径构成的导线框,半圆直径与磁场边缘重合;磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B0.使该线框从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流。现使线框保持图中所示位置,磁感应强度大小随时间线性变化。为了产生与线框转动半周过程中同样大小的电流,磁感应强度随时间的变化率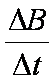
正确答案
解析
匀速转动时感应电动势与磁场变化时感应电动势相同即可。匀速转动时感应电动势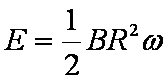
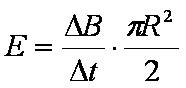
知识点
一矩形线框置于匀强磁场中,线框平面与磁场方向垂直,先保持线框的面积不变,将磁感应强度在1 s 时间内均匀地增大到原来的两倍,接着保持增大后的磁感应强度不变,在1 s 时间内,再将线框的面积均匀地减小到原来的一半,先后两个过程中,线框中感应电动势的比值为
正确答案
解析
本题考查感应电动势的计算。


知识点
有人设计了一种可测速的跑步机,测速原理如图所示,该机底面固定有间距为L、长度为d的平行金属电极,电极间充满磁感应强度为B、方向垂直纸面向里的匀强磁场,且接有电压表和电阻R.绝缘橡胶带上镀有间距为d的平行细金属条,磁场中始终仅有一根金属条,且与电极接触良好,不计金属电阻,若橡胶带匀速运动时,电压表读数为U,求:
(1)橡胶带匀速运动的速率;
(2)电阻R消耗的电功率;
(3)一根金属条每次经过磁场区域克服安培力做的功。
正确答案
(1)

解析
(1)设电动势为ε,橡胶带运动速率为v
由:ε=BLv,ε=U
得:v=
(2)设电功率为P
P=
(3)设电流强度为I,安培力为F,克服安培力做的功为W.
由:I =
得:W=
知识点
如图甲,一圆形闭合铜环由高处从静止开始下落,穿过一根竖直悬挂的条形磁铁,铜环的中心轴线与条形磁铁的中轴始终保持重合。若取磁铁中心O为坐标原点,建立竖直向下正方向的x轴,则图乙中最能正确反映环中感应电流i随环心位置坐标x变化的关系图像是
正确答案
解析
由楞次定律可知,感应线圈中电流方向变化,综合分析两个峰值不可能相等,由排除法可知正确答案选D
知识点
如图所示,质量

















(1)求框架开始运动时
(2)从



正确答案
(1)6m/s (2)1.1m
解析
(1)ab对框架的压力 
框架受水平面的支持力
依题意,最大静摩擦力等于滑动摩擦力,则框架受到最大静摩擦力

ab中的感应电动势E=
MN中电流 
MN受到的安培力 
框架开始运动时
由上述各式代入数据解得v=6m/s⑧
(2)闭合回路中产生的总热量: 
由能量守恒定律,得:
代入数据解得x=1.1m⑾
知识点
如图所示,两条平行的光滑金属导轨固定在倾角为θ的绝缘斜面上,导轨上端连接一个定值电阻。导体棒a和b放在导轨上,与导轨垂直开良好接触。斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场。现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒恰好静止。当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨。当a棒再次滑回到磁场上边界PQ处时,又恰能沿导轨匀速向下运动。已知a棒、b棒和定值电阻的阻值均为R,b棒的质量为m,重力加速度为g,导轨电阻不计。求
(1)a棒在磁场中沿导轨向上运动的过程中,a棒中的电流强度Ia与定值电阻中的电流强度Ic之比;
(2)a棒质量ma;
(3)a棒在磁场中沿导轨向上运动时所受的拉力F。
正确答案
见解析
解析
(1)






解得:
(2)由于







当


向上匀速运动时,



由以上各式联立解得:
(3)由题可知导体棒

知识点
如图,均匀带正电的绝缘圆环a与金属圆环b同心共面放置,当a绕O点在其所在平面内旋转时,b中产生顺时针方向的感应电流,且具有收缩趋势,由此可知,圆环a
正确答案
解析
由题意知:圆环a b电流方向相同,在安培力作用下体现出相互吸引的效果,且根据楞次定律“增反减同”原则,a环在减速旋转。
知识点
扫码查看完整答案与解析