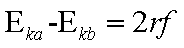- 电磁学
- 共4057题
制备纳米薄膜装置的工作电极可简化为真空中间距为



电压变化的周期为2r,如图乙所示.在t=0时,极板B附近的一个电子,质量为m、电荷量为e,受电场作用由静止开始运动.若整个运动过程中,电子未碰到极板A,且不考虑重力作用.
(1)若


(2)若电子在

(3)若电子在第
正确答案
见解析
解析
(1)电子在0~T时间内做匀加速运动
加速度的大小 
位移 
在T-2T时间内先做匀减速运动,后反向作匀加速运动
加速度的大小 
初速度的大小 
匀减速运动阶段的位移 
依据题意 



(2)在2nT~(2n+1)T,(n=0,1,2, ……,99)时间内 ⑦
加速度的大小 a′2=
速度增量 △v2=-a′2T ⑧
(a)当0≤t-2nt<T时
电子的运动速度 v=n△v1+n△v2+a1(t-2nT) ⑨
解得 v=[t-(k+1)nT] 
(b)当0≤t-(2n+1)T<T时
电子的运动速度 v=(n+1) △v1+n△v2-a′2[t-(2n+1)T] ⑪
解得v=[(n+1)(k+1)T-kl]
(3)电子在2(N-1)T~(2N-1)T时间内的位移x2N-1=v2N-2T+
电子在(2N-1)T~2NT时间内的位移x2N=v2N-1T-
由⑩式可知 v2N-2=(N-1)(1-k)T
由⑫式可知 v2N-1=(N-Nk+k)T
依据题意 x2N-1+ x2N=0
解得
知识点
如图,一半径为R的圆表示一柱形区域的横截面(纸面)。在柱形区域内加一方向垂直于纸面的匀强磁场,一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域,在圆上的b点离开该区域,离开时速度方向与直线垂直。圆心O到直线的距离为
正确答案
解析
粒子在磁场中做圆周运动,设圆周的半径为r,由牛顿第二定律和洛仑兹力公式得
① 式中v为粒子在a点的速度。
过b点和O点作直线的垂线,分别与直线交于c和d点。由几何关系知,线段


设


联立式得
再考虑粒子在电场中的运动。设电场强度的大小为E,粒子在电场中做类平抛运动。设其加速度大小为a,由牛顿第二定律和带电粒子在电场中受力公式得

粒子在电场方向和直线方向所走的距离均为r,由运动学公式得


式中t是粒子在电场中运动的时间,联立式得
知识点
质谱分析技术已广泛应用于各前沿科学领域。汤姆孙发现电子的质谱装置示意如图,M、N为两块水平放置的平行金属极板,板长为L,板右端到屏的距离为D,且D远大于L,


(1)设一个质量为







(2)假设你利用该装置探究未知离子,试依照以下实验
上述装置中,保留原电场,再在板间加沿


正确答案
(1)
解析
(1)离子在电场中受到的电场力 
离子获得的加速度 
离子在板间运动的时间 
到达极板右边缘时,离子在+y方向的分速度 
离子从板右端到达屏上所需时间 
离子射到屏上时偏离O点的距离
由上述各式,得 
(2)设离子电荷量为q,质量为m,入射时速度为v,磁场的磁感应强度为B,磁场对离子的洛伦兹力

已知离子的入射速度都很大,因而粒子在磁场中运动时闻甚短。所经过的圆弧与圆周相比甚小,且在板中运动时,OO'分逮度总是远大于在x方向和y方向的分速度,洛伦兹力变化甚微,顾可作恒力处理,洛伦兹力产生的加速度






离子飞出极板到达屏时,在


当离子的初速度为任意值时,离子到达屏上时的位置在



由⑩、⑾两式得

其中
上式表明,





故该未知离子的质量数为14。
知识点
如图,场强大小为E.方向竖直向下的匀强电场中有一矩形区域abcd,水平边ab长为s,竖直边ad长为h。质量均为m.带电量分别为+q和-q的两粒子,由a.c两点先后沿ab和cd方向以速率v0进入矩形区(两粒子不同时出现在电场中)。不计重力。若两粒子轨迹恰好相切,则v0等于( )
正确答案
解析
略
知识点
喷墨打印机的简化模型如图4所示,重力可忽略的墨汁微滴,经带电室带负电后,以速度v垂直匀强电场飞入极板间,最终打在纸上,则微滴在极板间电场中
正确答案
解析
A 不计重力的微滴带负电所受电场力方向指向带正电荷的极板故A错
B 在电场力方向做初速为零的匀加速直线运动,故粒子动能增加,电场力做正功,电势能减小,B错
C 不计重力的带负电微滴初速和恒定电场力垂直故轨迹为抛物线,C对
D 由



知识点
如图所示,待测区域中存在匀强电场和匀强磁场,根据带电粒子射入时的受力情况可推测其电场和磁场,图中装置由加速器和平移器组成,平移器由两对水平放置、相距为l的相同平行金属板构成,极板长度为l、间距为d,两对极板间偏转电压大小相等、电场方向相反,质量为m、电荷量为+q的粒子经加速电压U0加速后,水平射入偏转电压为U1的平移器,最终从A点水平射入待测区域,不考虑粒子受到的重力。
(1)求粒子射出平移器时的速度大小v1;
(2)当加速电压变为4U0时,欲使粒子仍从A点射入待测区域,求此时的偏转电压U;
(3)已知粒子以不同速度水平向右射入待测区域,刚进入时的受力大小均为F,现取水平向右为x轴正方向,建立如图所示的直角坐标系Oxyz,保持加速电压为U0不变,移动装置使粒子沿不同的坐标轴方向射入待测区域,粒子刚射入时的受力大小如下表所示。
请推测该区域中电场强度和磁感应强度的大小及可能的方向。
正确答案
见解析。
解析
(1)设粒子射出加速器的速度为v0
由动能定理qU0=
由题意得v1=v0,即
(2)在第一个偏转电场中,设粒子的运动时间为t
加速度的大小
在离开时,竖直分速度vy=at
竖直位移y1=
水平位移l=v1t
粒子在两偏转电场间做匀速直线运动,经历时间也为t
竖直位移y2=vyt
由题意知,粒子竖直总位移y=2y1+y2
解得
则当加速电压为4U0时,U=4U1。
(3)(a)由沿x轴方向射入时的受力情况可知:B平行于x轴,且
(b)由沿±y轴方向射入时的受力情况可知:E与Oxy平面平行。
F2+f2=
解得
(c)设电场方向与x轴方向夹角为α。
若B沿x轴方向,由沿z轴方向射入时的受力情况得
(f+Fsin α)2+(Fcos α)2=
解得α=30°或α=150°
即E与Oxy平面平行且与x轴方向的夹角为30°或150°。
同理,若B沿-x轴方向
E与Oxy平面平行且与x轴方向的夹角为-30°或-150°。
知识点
如图,ABD为竖直平面内的光滑
(1)甲乙两球碰撞后,乙恰能通过轨道的最高点D,求乙在轨道上的首次落点到B点的距离;
(2)在满足(1)的条件下。求的甲的速度υ0;
(3)若甲仍以速度υ0向右运动,增大甲的质量,保持乙的质量不变,求乙在轨道上的首次落点到B点的距离范围。
正确答案
(1)0.4m (2)
解析
(1)在乙恰能通过轨道的最高点的情况下,设乙到达最高点的速度为vD,乙离开D点到达水平轨道的时间为t,乙的落点到B点的距离为x,则



联立①②③得:
(2)设碰撞后甲.乙的速度分别为v甲.v乙,根据动量守恒和机械能守恒定律有:


联立⑤⑥得:v乙= v0 ⑦
由动能定理得:
联立①⑦⑧得:
(3)设甲的质量为M,碰撞后甲.乙的速度分别为vM.vm,根据动量守恒和机械能守恒定律有:


联立⑩11得: 
由12和

设乙球过D点的速度为

联立⑨1314得:
设乙在水平轨道上的落点到B点的距离为

联立②1516得:
知识点
如图(a)所示,两平行正对的金属板A、B间加有如图(b)所示的交变电压,一重力可忽略不计的带正电粒子被固定在两板的正中间P处。若在t0时刻释放该粒子,粒子会时而向A板运动,时而向B板运动,并最终打在A板上。则t0可能属于的时间段是
正确答案
解析
若0<t0<




知识点
反射式速调管是常用的微波器件之一,它利用电子团在电场中的振荡来产生微波,其振荡原理与下述过程类似。如图所示,在虚线MN两侧分别存在着方向相反的两个匀强电场,一带电微粒从A点由静止开始,在电场力作用下沿直线在A、B两点间往返运动。已知电场强度的大小分别是E1=2.0×103N/C和E2=4.0×103N/C,方向如图所示。带电微粒质量m=1.0×10-20kg,带电量q=-1.0×10-9C,A点距虚线MN的距离d1=1.0cm,不计带电微粒的重力,忽略相对论效应。求:
(1)B点到虚线MN的距离d2;
(2)带电微粒从A点运动到B点所经历的时间t。
正确答案
(1)0.50 cm
(2)1.5×10-8 s
解析
(1)带电微粒由A运动B的过程中,由动能定理有|q|E1d1-|q|E2d2 = 0
解得 d2 = 
(2)设微粒在虚线MN两侧的加速度大小分别为a1、a2,由牛顿第二定律有
|q|E1 = ma1
|q|E2 = ma2
设微粒在虚线MN两侧的时间大小分别为t1、t2,由运动学公式有
d1 =
d2 =
又t = t1+t2
解得t = 1.5×10-8 s
知识点
如图17所示,质量为M的导体棒ab,垂直放在相距为l的平行光滑金属轨道上。导轨平面与水平面的夹角为θ,并处于磁感应强度大小为B.方向垂直与导轨平面向上的匀强磁场中,左侧是水平放置.间距为d的平行金属板R和Rx分别表示定值电阻和滑动变阻器的阻值,不计其他电阻。
(1)调节Rx=R,释放导体棒,当棒沿导轨匀速下滑时,求通过棒的电流I及棒的速率v。
(2)改变Rx,待棒沿导轨再次匀速下滑后,将质量为m.带电量为+q的微粒水平射入金属板间,若它能匀速通过,求此时的Rx。
正确答案
见解析。
解析
(1)当ab匀速运动时 列力平衡方程得:Mgsinθ=BIl①
ab切割产生的电动势为:E=Blv②
由闭合欧姆定律得:
由①②③得:
(2)再次平衡时有:
Mgsinθ=BIl
由闭合欧姆定律得:
对微粒列平衡方程得:Eq=mg ⑥
U=IRx ⑦
由④——⑦得:
知识点
为了降低潜艇噪音,提高其前进速度,可用电磁推进器替代螺旋桨。潜艇下方有左、右两组推进器,每组由6个相同的用绝缘材料制成的直线通道推进器构成,其原理示意图如下。在直线通道内充满电阻率ρ=0.2Ω∙m的海水,通道中a×b×c=0.3m×0.4m×0.3m的空间内,存在由超导线圈产生的匀强磁场,其磁感应强度B=6.4T、方向垂直通道侧面向外。磁场区域上、下方各有a×b=0.3m×0.4m的金属板M、N,当其与推进器专用直流电源相连后,在两板之间的海水中产生了从N到M,大小恒为I=1.0×103A的电流,设电流只存在于磁场区域。不计电源内阻及导线电阻,海水密度ρ≈1.0×103kg/m3。
(1)求一个直线通道推进器内磁场对通电海水的作用力大小,并判断其方向;
(2)在不改变潜艇结构的前提下,简述潜艇如何转弯?如何“倒车”?
(3)当潜艇以恒定速度v0=30m/s前进时,海水在出口处相对于推进器的速度v=34m/s,思考专用直流电源所提供的电功率如何分配,求出相应功率的大小。
正确答案
见解析。
解析
(1)安培力的大小,F=BIL=6.4×1000×0.3=1.92×103N,
根据左手定则可知,方向:垂直于BI平面向右;
(2)开启或关闭不同个数的左、右两侧的直线通道推进器,实施转弯。
改变电流方向,或改变磁场方向,可以改变海水所受磁场力的方向,实施“倒车”。
(3)电源提供的电功率中的第一部分为牵引功率
P1=F牵v0=6.9×105W
电源提供的电功率中的第二部分为单位时间内海水的焦耳热功率
推进器内海水的电阻
电源提供的电功率中的第三部分为单位时间内海水动能的增加量
单位时间内通过推进器的水的质量为
m=ρmbcv水对地=480kg
单位时间内其动能增加为P3=
知识点
如图甲所示,静电除尘装置中有一长为L、宽为b、高为d的矩形通道,其前、后面板使用绝缘材料,上、下面板使用金属材料。图乙是装置的截面图,上、下两板与电压恒定的高压直流电源相连。质量为m、电荷量为-q、分布均匀的尘埃以水平速度v0进入矩形通道,当带负电的尘埃碰到下板后其所带电荷被中和,同时被收集。通过调整两板间距d可以改变收集效率η。当d=d0时η为81%(即离下板081d0范围内的尘埃能够被收集)。不计尘埃的重力及尘埃之间的相互作用。
(1)求收集效率为100%时,两板间距的最大值dm;
(2)求收集率η与两板间距d的函数关系;
(3)若单位体积内的尘埃数为n,求稳定工作时单位时间下板收集的尘埃质量ΔM/Δt与两板间距d的函数关系,并绘出图线。
正确答案
见解析。
解析
(1)收集效率

在竖直方向有
其中 
当减少两板间距是,能够增大电场强度,提高装置对尘埃的收集效率。收集效率恰好为100%时,两板间距为
因此,在水平方向有
在竖直方向有 
其中
联立①②③④⑤⑥可得
(2)通过前面的求解可知,当

当 

根据题意,收集效率为 
联立①②③⑨⑩可得
(3)稳定工作时单位时间下板收集的尘埃质量
当 


绘出的图线如下:
知识点
如图,在第一象限存在匀强磁场,磁感应强度方向垂直于纸面(xy平面)向外;在第四象限存在匀强电场,方向沿x轴负向。在y轴正半轴上某点以与x轴正向平行、大小为

(1)电场强度大小与磁感应强度大小的比值;
(2)该粒子在电场中运动的时间。
正确答案
见解析。
解析
(1)如图,粒子进入磁场后做匀速圆周运动。设磁感应强度的大小为B,粒子质量与所带电荷量分别为m和q,圆周运动的半径为

由题给条件和几何关系可知
设电场强度大小为E,粒子进入电场后沿x轴负方向的加速度大小为




由于粒子在电场中做类平抛运动(如图),有

联立①②③④⑤⑥式得

(2)联立⑤⑥式得

(评分参考:第(1)问18分,①式3分,②式1分,③④⑤⑥式各3分,⑦式2分;第(2)问2分,⑧式2分)
知识点
匀强电场的方向沿x轴正向,电场强度E随x的分布如图所示。图中E0和d均为已知量。将带正电的质点A在O点由能止释放,A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放,当B在电场中运动时,A. B间的相互作用力及相互作用能均为零。B离开电场后,A、B间的相作用视为静电作用,已知A的电荷量为Q,A和B的质量分别为m和1/4m,不计重力。
(1)求A在电场中的运动时间t;
(2)若B的电荷量
(3)为使B离开电场后不改变运动方向.求B所带电荷量的最大位qm;
正确答案
见解析。
解析
(1)由牛顿第二定律,A在电场中运动的加速度a=
A在电场中做匀变速直线运动 d=
解得运动时间 t=
(2)设A、B离开电场时的速度分别为υA0、υB0,由动能定理,有
QE0d=


A、B相互作用过程中,动量和能量守恒。A、B相互作用力为斥力,A受的力与其运动方向相同,B受的力与其运动方向相反,相互作用力对A做正功,对B做负功。A、B靠近的过程中,B的路程大于A的路程,由于相互作用力大小相等,相互作用力对B做功的绝对值大于对A做功的绝对值,因此相互作用力做功之和为负,相互作用能增加。所以,当A、B最接近时相互作用能最大,此时两者速度相同,设为υ′,有
(m+

Epm=(




已知=
相互作用能的最大值 Epm=
(3)考虑A、B在x > d区间的运动,由动量守恒、能量守恒,且在初态和末态均无相互作用,有:
mυA+







由④、⑤解得 υB=-

因B不改变运动方向,故 υB=-

由①、⑥解得 q≤
即B所带电荷量的最大值 qm=
知识点
如图,匀强电场中有一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行。a、b为轨道直径的两端,该直径与电场方向平行。一电荷为q(q>0)的质点沿轨道内侧运动.经过a点和b点时对轨道压力的大小分别为FNa和FNb不计重力,求电场强度的大小E、质点经过a点和b点时的动能。
正确答案
见解析
解析
解析:质点所受电场力的大小为f=qE,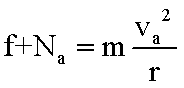
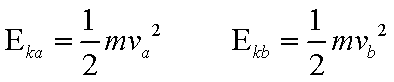
综上得: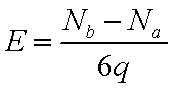
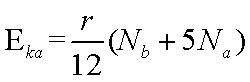
知识点
扫码查看完整答案与解析