- 等差数列的前n项和及其最值
- 共124题
19.已知数列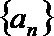
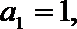
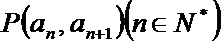
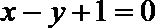
(1)求数列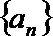
(2)若函数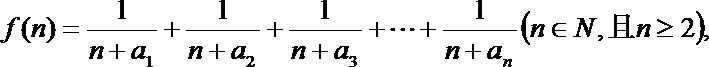
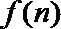
(3)设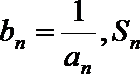
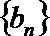
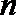
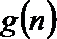
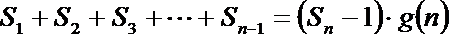
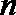
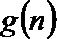
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列

正确答案
解析
当n=1时,a1=S1=9;
当n≥2时,an=Sn-Sn-1=11-2n,由于n=1时,a1=9也满足11-2n,因此an=11-2n.
(1)当n>5时,Tn=|a1|+|a2|+…+|an|=-Sn+2S5=n2-10n+50,
(2)当n≤5时,Tn=|a1|+|a2|+…+|an|=-(a1+a2+…+an)=10n-n2,
综合(1)(2),得Tn=
知识点
14.已知数列

正确答案
解析
当n=1时,a1=S1=9;
当n≥2时,an=Sn-Sn-1=11-2n,由于n=1时,a1=9也满足11-2n,因此an=11-2n.
(1)当n>5时,Tn=|a1|+|a2|+…+|an|=-Sn+2S5=n2-10n+50,
(2)当n≤5时,Tn=|a1|+|a2|+…+|an|=-(a1+a2+…+an)=10n-n2,
综合(1)(2),得Tn=
知识点
8.已知等差数列{an}的前n项和为Sn,若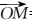
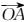
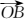
正确答案
2015
解析
若O、A、B、M为平面内四点,则A、B、M三点在一条直线上,当且仅当存在一对实数m、n,使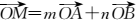
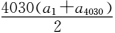
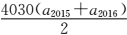
知识点
16.已知等差数列{an}的前n项和为Sn,若=a100+a101,且A、B、C三点共线(该直线不过点O),则S200等于________.
正确答案
100
解析
由条件可得a100+a101=1,即a1+a200=1,从而S200=100.故填100.
知识点
扫码查看完整答案与解析