- 等差数列的前n项和及其最值
- 共124题
18. 已知数列


(Ⅰ)求

(Ⅱ)设



正确答案
(1)


解析
试题分析:本题属于等差数列及数列的求和,
(1)直接利用公式来解答;
(2)先利用裂项相消法求出
(Ⅰ)设数列


由

所以

(Ⅱ)可得

由于

即

考查方向
解题思路
本题考查等差数列及数列的求和,解题步骤如下:(1)直接利用公式来解答;(2)先利用裂项相消法求出
易错点
第二问求和不晓得使用裂项相消法去做。
知识点
已知等差数列



16.求
17.设等比数列






正确答案
(Ⅰ)
解析
试题分析:(Ⅰ)由已知及等差数列的通项公式和前n项和公式可得关于数列的首项a1和公式d的二元一次方程组,解此方程组可求得首项及公差的值,从而可写出此数列的通项公式.
试题解析: (1)设

化简得
解得
故通项公式

考查方向
解题思路
本题考查等差数列的概念、通项公式及前n项的求和公式,利用方程组思想求解.本题属于基础题.
易错点
等差数列性质的运用
正确答案

解析
试题分析: (Ⅱ)由(Ⅰ)的结果可求出b1和b4的值,进而就可求出等比数列的公比,再由等比数列的前n项和公式



设


故

考查方向
解题思路
本题考查等比数列的概念、通项公式及前n项的求和公式,利用方程组思想求解.本题属于基础题.
易错点
注意运算的准确性
7.

正确答案
解析
根据题意可得,
化简可得

故选C.
考查方向
解题思路
根据

易错点
无
知识点
6.设数列





正确答案
解析
根据题意可得,



考查方向
等差数列的性质
解题思路
根据题意建立等量关系,求出首项和公差,然后求出A20的值
易错点
等差数列的性质掌握不好,解方程错误
知识点
13.设等差数列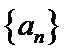
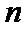
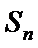
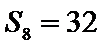

正确答案
16
解析
由题意可知,
考查方向
等差数列的前n项和
解题思路
根据等差数列的性质,求出答案
易错点
不理解等差数列的性质和运算
知识点
扫码查看完整答案与解析