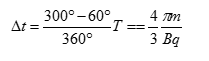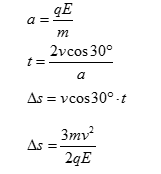热门试卷

在竖直平面内存在如图所示的绝缘轨道，一质量为m=0.4kg、带电量为q=+0.4C的小滑块(可视为质点)在外力作用下压缩至离B点0.05m，此时弹性势能=17.25J，弹簧一端固定在底端，与小滑块不相连，弹簧原长为2.05m，轨道与滑块间的动摩擦因数．某时刻撤去外力，经过一段时间弹簧恢复至原长，再经过1.8s，同时施加电场和磁场，电场平行于纸面，且垂直x轴向上，场强E=10N/C；磁场方向垂直于纸面，且仅存在于第二、三象限内，最终滑块到达N(6m，0)点，方向与水平方向成30º斜向下．(答案可用π表示，)

⑴求弹簧完全恢复瞬间，小滑块的速度；

⑵求弹簧原长恢复后1.8s时小滑块所在的位置；

⑶求小滑块在磁场中的运动的时间．

26．如图所示，在以坐标原点O为圆心，半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里。一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经t0时间从P点射出。

（1）求电场强度的大小和方向。

（2）若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。

（3）若仅撤去电场，带电粒子仍从O点射入，且速度为原来的4倍，求粒子在磁场中运动的时间。

25．如图所示，条形区域I内存在垂直于纸面向外的匀强磁场，磁感应强度B1=0．3 T，Ⅱ内存在垂直于纸面向里的匀强磁场，磁感应强度B2=B1，BB'、CC'间存在沿纸面方向竖直向下的匀强电场E，AA'、BB'、CC'、DD'为磁场边界，它们相互平行，条形区域的长度足够长，磁场宽度及BB'、CC'之间的距离d=1 m．一束带正电的某种粒子从AA'上的O点以沿与AA'成60°角以射人磁场，刚好垂直边界BB'射出区域I而进入匀强电场，且沿与CC'成60°角进入区域Ⅱ，最后粒子刚好不能从磁场区域Ⅱ射出，取≈3，不计粒子所受重力．求：

（1）粒子的比荷；

（2）电场强度E的大小；

（3）粒子从O到DD'所用的时间。（保留两位有效数字）

25.如图，在xoy直角坐标系中，在第三象限有一平行x轴放置的平行板电容器，板间电压。现有一质量，带电量的带正电的粒子(不计重力)，从下极板处由静止开始经电场加速后通过上板上的小孔，垂直x轴从A点进入第二象限的匀强磁场中。磁场方向垂直纸面向外，磁感应强度B=1T。粒子在磁场中转过四分之一圆周后又从B点垂直y轴进入第一象限，第一象限中有平行于y轴负方向的匀强电场E，粒子随后经过x轴上的C点，已知OC=1m。求：

（1）粒子在磁场中做匀速圆周运动的半径r。

（2）第一象限中匀强电场场强E的大小。

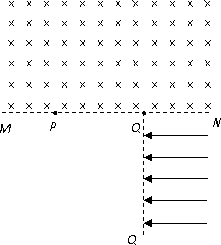
25．如图所示，在虚线MN的上方存在方向垂直纸面向里，磁感应强度为B的匀强磁场．在

MN的下方垂直MN的虚线QQ′右侧存在方向水平向左，场强为E的匀强电场．现有两个完全相同的带正电的粒子从MN上的P点先后以大小相同的速度v垂直磁场方向进入匀强磁场，结果同时经过MN上的Q点离开磁场，已知粒子的质量为m，带电量为q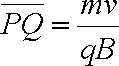，．不计重力和粒子间的相互作用力，

求：

（1）两粒子先后进入磁场的时间间隔；

（2）两粒子离开Q点后经多长时间相距最远，最远距离为多少？

26．如图所示，整个空间中存在竖直方向的匀强电场，场强大小，在 轴下方存在两个相邻的匀强磁场区域Ⅰ、Ⅱ，磁场区域Ⅰ的宽度，磁感应强度，方向垂直纸面向里，磁场区域Ⅱ的磁场方向垂直纸面向外。质量为电荷量为的带正电微粒在轴上P点由静止释放，经过一段时间，进入磁场区域Ⅰ。通过控制装置，使质点每次通过轴时，都使电场反向一次，但电场强度的大小不变。带电微粒在磁场区域Ⅰ中，速度方向改变时，进入磁场区域Ⅱ。已知，，。

（1）求P点的坐标；

（2）如果要使微粒能返回P点，求磁场区域Ⅱ磁感应强度的值和粒子从开始运动到第一次返回P点所需的时间。

26.如图所示，相距3L的AB、CD两直线间的区域存在着两个大小不同、方向相反的有界匀强电场，其中PT上方的电场I的场强方向竖直向下，PT下方的电场II的场强方向竖直向上，电场I的场强大小是电场Ⅱ的场强大小的两倍，在电场左边界AB上有点Q，PQ间距离为L。从某时刻起由Q以初速度v0沿水平方向垂直射入匀强电场的带电粒子，电量为＋q、质量为m。通过PT上的某点R进入匀强电场I后从CD边上的M点水平射出，其轨迹如图，若PR两点的距离为2L。不计粒子的重力。试求：

（1）匀强电场I的电场强度E的大小和MT之间的距离；

（2）有一边长为a、由光滑弹性绝缘壁围成的正三角形容器，在其边界正中央开有一小孔S，将其置于CD右侧且紧挨CD边界，若从Q点射入的粒子经AB、CD间的电场从S孔水平射入容器中。欲使粒子在容器中与器壁多次垂直碰撞后仍能从S孔射出(粒子与绝缘壁碰撞时无机械能和电量损失)，并返回Q点，需在容器中现加上一个如图所示的匀强磁场，粒子运动的半径小于a/2，求磁感应强度B的大小应满足的条件以及从Q出发再返回到Q所经历的时间。

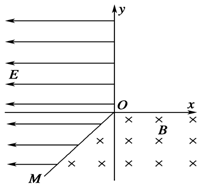
25．在xOy平面内，第Ⅲ象限内的直线OM是电场与磁场的边界，OM与x轴负方向成45°角。

在x<0且OM的左侧空间存在着x轴负方向的匀强电场，场强大小为E=50N/C，在y<0且OM

的右侧空间存在着垂直纸面向里的匀强磁场，磁感应强度的大小为B=0.2T，如图所示。一

不计重力的带负电的微粒，从坐标原点O沿y轴负方向以v0＝4×103m/s的初速度进入磁场，

已知微粒的带电荷量为q＝-4×10－18C，质量为m＝1×10－24kg。求：

（1）带电微粒第一次经过磁场边界时的位置坐标及经过磁场边界时的速度方向；

（2）带电微粒最终离开电、磁场区域时的位置坐标；

（3）带电微粒在电、磁场区域运动的总时间(结果可以保留)。

25.如图所示，在xOy平面中第一象限内有一点P(4，3)，OP所在直线下方有垂直于纸面向里的匀强磁场，OP上方有平行于OP向上的匀强电场，电场强度E＝100V/m。一质量m＝1×10－6kg，电荷量q＝2×10－3C带正电的粒子，从坐标原点O以初速度v＝1×103m/s垂直于磁场方向射入磁场，经过P点时速度方向与OP垂直并进入电场，在经过电场中的M点(图中未标出)时的动能为P点时动能的2倍，不计粒子重力。求：

（1）磁感应强度的大小；

（2）O、M两点间的电势差；

（3）M点的坐标及粒子从O运动到M点的时间。