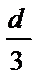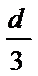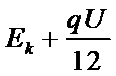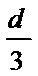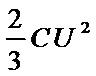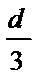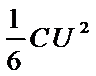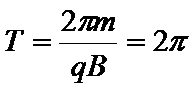- 带电粒子在混合场中的运动
- 共247题
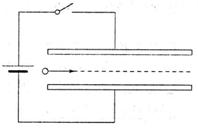
8.如图所示,平行板电容器两极板水平放置,一电容为C。电容器与一直流电源相连,初始时开关闭合,极板间电压为U,两极板间距为d,电容器储存的能量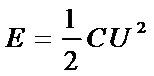
正确答案
解析
A、保持开关闭合,电压不变,仅将上极板下移
的过程中,极板距离减小,根据场强公式可知电场强度增大,电场力增大,带电油滴做曲线运动,故A错误;
B、保持开关闭合,仅将上极板下移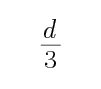
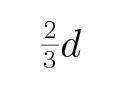
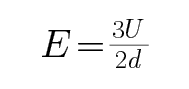
开始油滴沿直线运动,则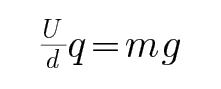
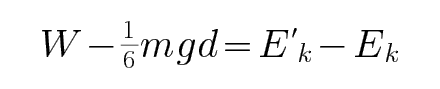
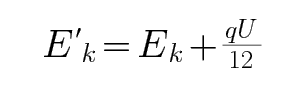
CD、开始时电容器储存的能量为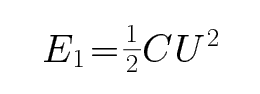
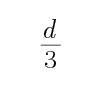
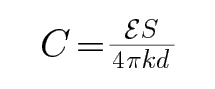
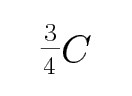
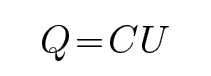
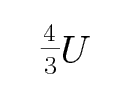
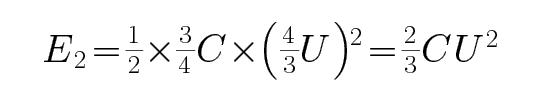
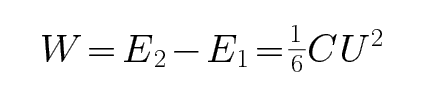
考查方向
带电粒子在匀强电场中的运动
解题思路
带电油滴受到重力和电场力处于平衡,当电场强度增大时,液滴将会向上运动.电容器始终与电源相连,两端的电压不变,电容器与电源断开,所带的电量不变,根据动态分析判断电场强度的变化.
易错点
掌握电容器始终与电源相连,两端的电压不变,电容器与电源断开,所带的电量不变.
知识点
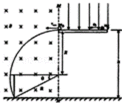
7.磁流体发电机,又叫等离子体发电机,下图中的燃烧室在3000K的高温下将气体全部电离为电子与正离子,即高温等离子体。高温等离子体经喷管提速后以1000m/s进入矩形发电通道,发电通道有垂直

正确答案
解析
A、由等离子体所受的电场力和洛伦兹力平衡得:
B、由上知,发电机的电动势与高速等离子体的电荷量无关,即与离子的化合价无关,由E=Bdv能求电动势,故B错误;
C、发动机的内阻为:

D、当电源的内外电阻相等时输出功率最大,此时外电阻为 R=r=4Ω,故D正确.
考查方向
电功、电功率; 电源的电动势和内阻; 闭合电路欧姆定律
解题思路
根据等离子体所受的电场力和洛伦兹力平衡,列式求电动势.发动机的效率等于输出功率与总功率之比.当电源的内外电阻相等时输出功率最大.
易错点
当等离子体所受的电场力和洛伦兹力平衡,由此求出电动势是解题关键.
知识点
如图所示,在平行于水平地面的匀强磁场中,有一小球质量为m,带电量为+q,磁场的磁感应强度为B,小球离地足够高,初速度为零。求:
29.小球下落到最底点时,其轨迹在该点的曲率半径是多少?(提示曲线的曲率半径是曲线上该点的最大内切圆或最小外切圆的半径)
30.小球下落的最大距离是多少?
31.小球下落过程中重力做功的最大功率为多大?
正确答案
正确答案
正确答案
如图所示,在真空中,沿水平方向和竖起方向建立直角坐标系xOy,在x轴上方有一沿x轴正方向的匀强电场E(电场强度E的大小未知)。有一质量为m,带电量为+q的小球,从坐标原点O由静止开始自由下落,当小球运动到P(0,-h)点时,在x轴下方突然加一竖直向上的匀强电场,其电场强度与x轴上方的电场强度大小相等,且小球从P返回到O点与从O点下落到P点所用的时间相等。重力加速度为g。试求:
27.小球返回O点时速度的大小;
28.匀强电场的电场强度E的大小;
29.小球运动到最高点时的位置坐标。
正确答案
解析
设小球从O点运动到P点所用时间为t,在P点的速度为v1,返回O点时的速度为v2,则





考查方向
考查带电物体在电场中的运动:这类问题电场只是提供了一个电场力,可以转化为动力学问题求解,联系公式:
解题思路
首先分析小球从O点下落到P点再到O点的运动类型,明确这是两个阶段,应该分开分析,根据时间相等,及位移相等,解得小球回到O点时的速度。
易错点
在做运动学问题时,对公式的选择模糊不清,导致浪费时间,甚至解答困难。
正确答案
解析
(2)


考查方向
解题思路
根据运动学的基本公式解得小球在电场作用下的加速度a,再根据qE-mg=ma,解得E的大小。
易错点
在做运动学问题时,对公式的选择模糊不清,导致浪费时间,甚至解答困难。
正确答案
位置坐标为(4h,16h)
解析
在竖直方向:



考查方向
解题思路
小球进入x轴上方时,将小球的运动分解成竖直方向和水平方向,小球在竖直方向上做减速度为g的减速运动,在水平方向上在电场力作用下做匀加速运动,分别根据运动学公式计算两个方向的位移,得出小球的最高位置坐标。
易错点
在做运动学问题时,对公式的选择模糊不清,导致浪费时间,甚至解答困难。
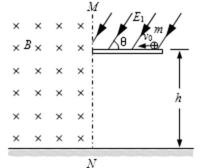
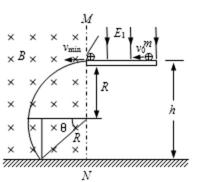
如图所示,水平地面上方竖直边界MN左侧存在垂直纸面向里的匀强磁场B和沿竖直方向的匀强电场E2(未画出),磁感应强度B=1.0 T,MN边界右侧离地面h= 3m处有长为L=0.91 m的光滑水平绝缘平台,平台的左边缘与MN重合,平台右边缘有一质量m=0.l kg、电量q=0.1C的带正电小球,以初速度v0=0.6m/s向左运动。此时平台上方存在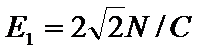
18.电场强度E2的大小和方向。
19.小球离开平台左侧后在磁场中运动的最短时间。
20.小球离开平台左侧后,小球落地点的范围。
正确答案
(1)电场强度E2的大小为10N/C,方向:竖直向上;
解析
(1)因为小球做匀速圆周运动,电场力必等于重力
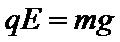
将数据代入①式解得: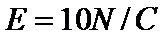
电场的方向竖直向上
考查方向
解题思路
(1)小球做匀速圆周运动,电场力等于重力,据此求出场强.
易错点
本题是小球在重力场、电场与磁场的复合场中运动类型,考查受力平衡的状态方程,机械能守恒与动量守恒定律的应用,关键要把握每个过程遵守的物理规律,结合几何知识进行处理.
正确答案
(2)小球离开平台左侧后在磁场中运动的最短时间为0.21s;
解析
(2)若θ=90°,小球匀速通过MN后有最小速度: 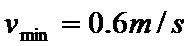
若θ=45°,小球匀速通过MN后有最大速度,由加速度公式可得:
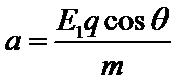
由匀变速直线运动规律可得: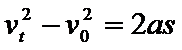
将数据代入④⑤式,可解得: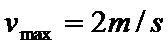
小球在通过MN的速度为大于等于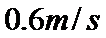
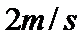
小球以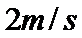
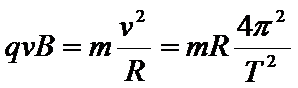
由⑦式可得: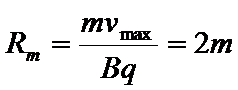
由⑦式解得:
因为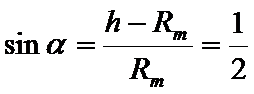
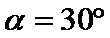
考查方向
解题思路
(2)小球在磁场中做匀速圆周运动,求出小球做圆周运动的圆心角,然后求出其运动时间.
易错点
本题是小球在重力场、电场与磁场的复合场中运动类型,考查受力平衡的状态方程,机械能守恒与动量守恒定律的应用,关键要把握每个过程遵守的物理规律,结合几何知识进行处理.
正确答案
(3)小球离开平台左侧后,小球落地点的范围是:在N点左边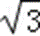
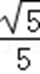
解析
(3)小球落在N点左边的最大距离时,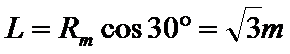
当小球落在右边最大距离时其对应在磁场中的轨道半径为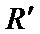
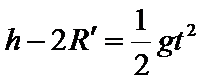
水平位移为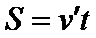
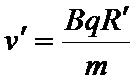
因此得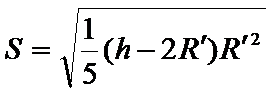
当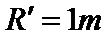
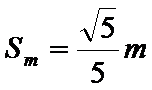
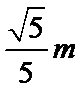
所以,小球的落点在距N点左边1.73m、右边0.447m的范围内
考查方向
解题思路
(3)求出小球落地点最左侧距离,然后求出落地点的右侧距离,然后确定其落地点范围.
易错点
本题是小球在重力场、电场与磁场的复合场中运动类型,考查受力平衡的状态方程,机械能守恒与动量守恒定律的应用,关键要把握每个过程遵守的物理规律,结合几何知识进行处理.
如图,在真空中竖直平面内同时存在多层厚度为d,足够宽的正交复合场,匀强电场的电场强度大小为



29.求小球在第1层复合场区域做圆周运动的轨道半径
30.求小球到达第2个复合场区域时速度方向与竖直方向夹角的正弦值;
31.若空间存在有n层复合场,小球不能从复合场下边界穿出,求n的最小值。
正确答案

解析
小球进入第1层复合场时,只有重力做功,由动能定理得:
在复合场中小球受重力与电场力相等,洛仑兹力提供圆周运动向心力,有:
联立解得:
考查方向
动能定理;带电粒子在匀强磁场中的运动
解题思路
由动能定理先求粒子进入第一层复合场的速度,进入复合场后,带电粒子在洛伦兹力提供向心力下在磁场中做匀速圆周运动.
易错点
本题关键要分析出当粒子进入复合场时,粒子做匀速圆周运动.
正确答案

解析
设从第1层复合场穿出时速度与竖直方向夹角为



设从第2层复合场进入时速度与竖直方向夹角为
根据动能定理
联立解得 :
考查方向
动能定理;带电粒子在匀强磁场中的运动
解题思路
由几何关系表示出从第1层复合场穿出时速度与竖直方向夹角,同理根据动能定理求出进入第1层复合场时速度的大小,在由几何关系表示出粒子进入第2层复合场时速度与竖直方向夹角,找两个角之间的关系;
易错点
本题关键是做出粒子的运动轨迹示意图,由几何关系求解.
正确答案

解析
设从第n层复合场进入时速度与竖直方向夹角为


小球在重力场中运动时,垂直于重力方向的速度分量不变,则:
联立得: 


根据动能定理


联立解得
考查方向
动能定理;带电粒子在匀强磁场中的运动
解题思路
根据几何关系找出从第n层复合场进入时的半径与d之间的关系,根据动能定理与牛顿第二定律求解.
易错点
进入第n层时粒子做匀速圆周运动的半径与d之间的关系是解决问题的关键.
容器A中装有大量的质量、电量不同但均带正电的粒子,粒子从容器下方的小孔 Sl不断飘人加速电场(初速度可视为零)做直线运动通过小孔S2后,从两平行板中央垂直电场方向射人偏转电场。粒子通过平行板后垂直磁场方向进入磁感应强度为B,方向垂直向里的匀强磁场区域,最后打在感光片上,如图所示。已知加速场S1、S2间的加速电压为 u,偏转电场极板长为L,两板间距也为L,板间匀强电场强度E=

26.粒子射入磁场时,其速度方向与边界ab间的夹角;
27.射到感光片Q处的粒子的比荷(电荷量与质量之比);
28.粒子在磁场中运动的最短时间。
正确答案
(1)
解析
(1)设质量为m,电量为q的粒子通过孔S2的速度为v0

粒子在平行板间:


联解①②③④得:
其速度方向与边界ab间的夹角
考查方向
解题思路
根据动能定理求出粒子经加速电场时的速度,粒子在偏转电场中做类平抛运动,求出其速度方向与边界ab间的夹角,由带电粒子在匀强磁场中的圆周运动确定出半径,然后求出射到感光片Q处的粒子的比荷,由粒子在磁场中运动的偏转角,求出粒子在磁场中运动的最短时间。
易错点
粒子射入磁场时的速度应为合速度,由几何关系确定粒子的运动半径大小,粒子在磁场中运动的偏转角的求解问题。
正确答案
(2)
解析
粒子从e板下端与水平方向成450的角射入匀强磁场。
设质量为m。
电量为q的粒子射入磁场时的速度为v,
做圆周运动的轨道半径为r

由可知:


联解⑤⑥⑦得:
粒子的比荷为:
考查方向
解题思路
根据动能定理求出粒子经加速电场时的速度,粒子在偏转电场中做类平抛运动,求出其速度方向与边界ab间的夹角,由带电粒子在匀强磁场中的圆周运动确定出半径,然后求出射到感光片Q处的粒子的比荷,由粒子在磁场中运动的偏转角,求出粒子在磁场中运动的最短时间。
易错点
粒子射入磁场时的速度应为合速度,由几何关系确定粒子的运动半径大小,粒子在磁场中运动的偏转角的求解问题。
正确答案
(3)
解析
设粒子在磁场中运动的时间为t


联解⑧⑨得:
因为所有粒子在磁场中运动的偏转角
所以粒子打在P处时间最短由几何知:r2+r2=L2 
联解⑩⑪得
粒子在磁场中的最短时间
考查方向
解题思路
根据动能定理求出粒子经加速电场时的速度,粒子在偏转电场中做类平抛运动,求出其速度方向与边界ab间的夹角,由带电粒子在匀强磁场中的圆周运动确定出半径,然后求出射到感光片Q处的粒子的比荷,由粒子在磁场中运动的偏转角,求出粒子在磁场中运动的最短时间。
易错点
粒子射入磁场时的速度应为合速度,由几何关系确定粒子的运动半径大小,粒子在磁场中运动的偏转角的求解问题。
扫码查看完整答案与解析