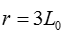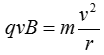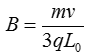热门试卷

25.如图14所示，在xOy平面内，以O′(0，R)为圆心、R为半径的圆内有垂直平面向外的匀强磁场，x轴下方有垂直平面向里的匀强磁场，两区域磁感应强度大小相等．第四象限有一与x轴成45°角倾斜放置的挡板PQ，P、Q两点在坐标轴上，且O、P两点间的距离大于2R，在圆形磁场的左侧0<y<2R的区间内，均匀分布着质量为m、电荷量为＋q的一簇带电粒子，当所有粒子均沿x轴正向以速度v射入圆形磁场区域时，粒子偏转后都从O点进入x轴下方磁场，结果有一半粒子能打在挡板上．不计粒子重力、不考虑粒子间相互作用力．

求：

（1）磁场的磁感应强度B的大小；

（2）挡板端点P的坐标；

（3）挡板上被粒子打中的区域长度．

25.如图10所示,空间分布着有理想边界的匀强电场和匀强磁场,左侧匀强电场的场强大小为E、方向水平向右，其宽度为L；中间区域匀强磁场的磁感应强度大小为B、方向垂直纸面向外；右侧匀强磁场的磁感应强度大小也为B、方向垂直纸面向里。一个带正电的粒子（质量m,电量q,不计重力）从电场左边缘a点由静止开始运动，穿过中间磁场区域进入右侧磁场区域后，又回到了a点，然后重复上述运动过程。（图中虚线为电场与磁场、相反方向磁场间的分界面，并不表示有什么障碍物）。求：

（1）带电粒子进入磁场时的速度大小；

（2）中间磁场区域的宽度d为多大；

（3）带电粒子从a点开始运动到第一次回到a点时所用的时间t.

25．如图所示，两平行金属板A、B长l＝8cm，两板间距离d＝8cm，B板比A板电势高300V，即UBA＝300V。一带正电的粒子电量q＝10-10C，质量m＝10-20kg，从R点沿电场中心线垂直电场线飞入电场，初速度v0＝2×106m/s，粒子飞出平行板电场后经过无场区域后，进入界面为MN、PQ间匀强磁场区域，从磁场的PQ边界出来后刚好打在中心线上离PQ边界4L/3处的S点上。已知MN边界与平行板的右端相距为L,两界面MN、PQ相距为L,且L＝12cm。求（粒子重力不计）

（1）粒子射出平行板时的速度大小v；

（2）粒子进入界面MN时偏离中心线RO的距离多远？

（3）画出粒子运动的轨迹，并求匀强磁场的磁感应强度B的大小。

26．如图甲所示，两平行金属板A、B的板长l=0．20m，板间距d=0．20m，两金属板间加如图乙所示的交变电压，并在两板间形成交变的电场，忽略其边缘效应．在金属板右侧有一方向垂直于纸面向里的匀强磁场．其左右宽度D=0．40 m，上下范围足够大，边界MN和PQ均与金属板垂直．匀强磁场的磁感应强度．现从t=0开始，从两极板左端的中点O处以每秒1000个的速率不停地释放出某种带正电的粒子，这些粒子均以的速度沿两板间的中线OO′射入电场，已知带电粒子的比荷，粒子的重力和粒子间的相互作用都忽略不计，在粒子通过电场区域的极短时间内极板间的电压可以看作不变，。问：

（1）t=0时刻进入的粒子，经边界MN射入磁场和射出磁场时两点间的距离是多少？

（2）当AB板间电压满足什么条件时，带电粒子可以进入磁场？在电压变化的第一个周期内有多少个带电的粒子能进入磁场？

（3）何时由O点进入的带电粒子在磁场中运动的时间最长？最长时间为多少？（π≈3）

26．如图所示，一带电粒子先以某一速度在竖直平面内做匀速直线运动，经过一段时间后进入一磁场方向垂直于纸面向里、磁感应强度大小为B的圆形匀强磁场区域（图中未画出该磁场区域），粒子飞出磁场后垂直电场方向进入宽为L的匀强电场，电场强度的大小为E、方向竖直向上。当粒子穿出电场时速率变为原来的倍，已知带电粒子的质量为m、电荷量为q、重力不计，粒子进入磁场前的速度与水平方向成θ＝60°角。求：

（1）粒子的电性；

（2）带电粒子在磁场中运动时的速度大小；

（3）该圆形磁场区域的最小面积。

26．如图所示，在第一象限有一沿方向的匀强电场，在轴下方分布有两个匀强磁场区域、（、大小未知，方向均垂直于平面向外），以直线为分界线一质量为，电量为的带电粒子以平行于轴的速度从轴上P点射入电场后，在轴上的Q点处进入磁场区域；，；在直线上有一点M，，现在之间放一绝缘弹性板，板长略小于（不影响粒子在、两点的运动），粒子与板碰后反弹，沿板方向的分速度不变，垂直板的方向分速度与碰前大小相等方向相反，带电粒子电量不变、重力不计

（1）求粒子进入磁场时的速度大小和方向；

（2）粒子恰好从M点离开右侧磁场区域，求大小的可能取值；

（3）粒子由M点进入左侧磁场区域后，不再打板，而是直接垂直穿过轴上的N点，求粒子从P点运动到N点的过程中所用的时间

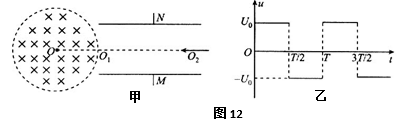
26．如图12甲所示，在真空中，虚线所围的圆形区域内存在范围足够大的匀强磁场，磁场方向垂直纸面向里。在磁场右侧有一对平行板M和N，两板间距离为6 L0,板长为12 L0，板的中心线O1O2与磁场的圆心O在同一直线上且O1恰在磁场边缘。给M、N板上加上如图乙所示的电压，电压大小恒为U0，周期大小可调。在t=0时刻，有一电荷量为q、质量为m的带电粒子，从M、N板右侧沿板的中心以大小为v的速度向左射入M、N之间，粒子刚好以平行于M、N板的速度穿出电场。（不计粒子重力）

（1）求周期T应该满足的条件？

（2）若粒子恰好从金属板的左边缘沿平行板的速度离开电场，进入磁场后又能平行于M、N极板返回电场，求磁场磁感应强度B的大小。