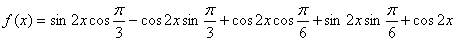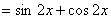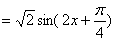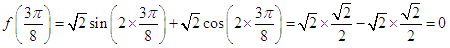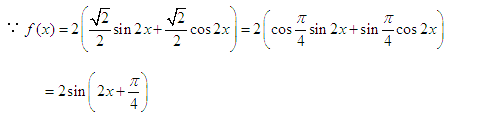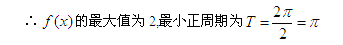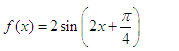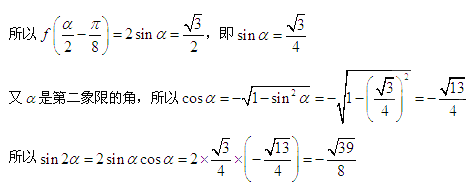- 三角函数的周期性及其求法
- 共111题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数f(x)=(2cos2x-1)sin 2x+
(1)求f(x)的最小正周期及最大值;
(2)若α∈

正确答案
(1)f(x)的最小正周期为

(2)
解析
(1)因为f(x)=(2cos2x-1)sin 2x+
=cos 2xsin 2x+
=
=
所以f(x)的最小正周期为

(2)因为f(α)=

因为α∈


所以

知识点
已知函数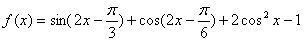
(1)求函数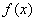
(2)求函数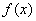
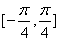
正确答案
见解析。
解析
(1)
所以函数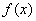
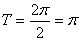
(2)因为
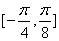

又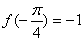
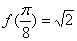
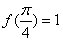
故函数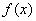
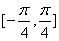
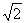
知识点
已知函数
(1)求函数
(2)若

正确答案
(1)f(x)的最小正周期为2
(2)
解析
(1)由已知,f(x)=
所以f(x)的最小正周期为2

(2)由(1)知,f(
所以cos(
所以

知识点
已知向量

(1) 求f (x)的最小正周期.
(2)求f (x) 在
正确答案
见解析
解析
(1) 

最小正周期
所以

(2)

所以,f (x) 在

知识点
已知函数

正确答案
解析
略
知识点
函数f(x)=2sin(ωx+φ)
正确答案
解析
由图象知函数周期T=2
∴ω=



∴


又

故选A。
知识点
函数f(x)=cos(2x+
正确答案
解析
根据复合三角函数的周期公式
函数f(x)=cos(2x+
知识点
已知函数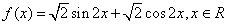
(1)求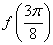
(2)求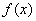
(3)若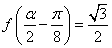
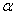
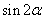
正确答案
见解析。
解析
(1)
(2)
(3)
由(2)可知
知识点
已知函数

(1)求
(2)已知



正确答案
见解析
解析
(1)




(2)证明:由已知得
两式相加得



∴
知识点
扫码查看完整答案与解析