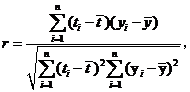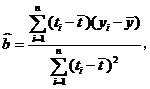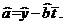线性回归方程_章节学习

1

题型：简答题

|

简答题 · 12 分

18.

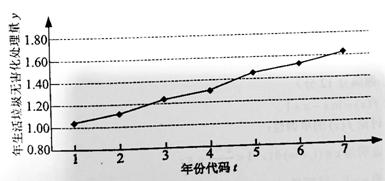
下图是我国2008年至2014年生活垃圾无害化处理量（单位：亿吨）的折线图。

注：年份代码1~7分别对应年份2008~2014.

（Ⅰ）由折线图看出，可用线性回归模型拟合y与t的关系，请用相关系数加以说明；

（Ⅱ）建立y关于t的回归方程（系数精确到0.01），预测2016年我国生活垃圾无害化处理量.

附注：

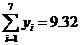
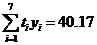
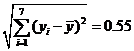
参考数据：，，，≈2.646.

参考公式：

回归方程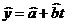中斜率和截距的最小二乘估计公式分别为：

正确答案

（Ⅰ）由折线图中数据和附注中参考数据得

，，，

，

. ........4分

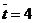
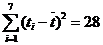
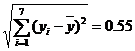
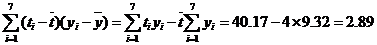
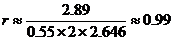
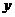
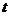
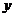
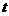
因为与的相关系数近似为0.99，说明与的线性相关程度相当高，从而可以用线性回归模型拟合与的关系. ............6分

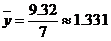
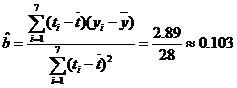
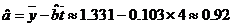
（Ⅱ）由及（Ⅰ）得，

.

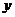
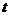
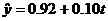
所以，关于的回归方程为：. ..........10分

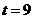
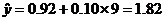
将2016年对应的代入回归方程得：.

所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨. .........12分

知识点

线性回归方程回归分析

1

题型：简答题

|

简答题 · 12 分

18.某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间（个月）和市场占有率（）的几组相关对应数据；

（1）根据上表中的数据，用最小二乘法求出关于的线性回归方程；

（2）根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过（精确到月）

附：.

正确答案

（1）见下面解析；（2）13个月。

解析

试题分析：本题属于线性回归方程，

（1）直接按照步骤来求；

（2）由第一问计算出来的线性回归方程然后直接利用即可解出来。

由，解得

预计上市13个月时，市场占有率能超过

考查方向

本题考查了线性回归方程。

解题思路

本题考查线性回归方程，解题步骤如下：

（1）直接按照步骤来求；

（2）由第一问计算出来的线性回归方程然后直接利用即可解出来。

易错点

求解回归方程时候容易计算出错。

知识点

线性回归方程回归分析的初步应用

1

题型：单选题

|

单选题 · 5 分

5．某洗发水的广告费用x与销售额y的统计数据如下表所示,根据表中数据可得回归方程中的b=2, 据此模型预报广告费用为15万元时销售额为( )

A48万元

B46万元

C44万元

D42万元

正确答案

C

解析

由表中数据得：。由于直线过点，且b=20，解得：

从而线性回归方程为，于是当时，得,故选C。

由表中数据得：。由于直线过点，且b=2，解得：

从而线性回归方程为，于是当时，得,故选C。

考查方向

本题主要考查了线性回归分析。

解题思路

根据回归直线方程过样本的中心点即可解出。

易错点

不知道考查的知识点是什么。

知识点

线性回归方程

1

题型：单选题

|

单选题 · 5 分

5.一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了4次试验，收集数据如右表示：根据右表可得回归方程中的为9.4，据此可估计加工零件数为6时加工时间大约为

A63.6 min

B65.5 min

C67.7 min

D72.0 min

正确答案

B

解析

由题中给出的表格得，由回归方程过得到，所以回归直线为，据此可估计加工零件数为6时加工时间大约为，故选B。

考查方向

本题主要考查回归直线的性质等知识，意在考查考生对于回归直线基本知识的掌握程度和运算求解能力。

解题思路

先求出样本点的中心，根据回归直线过样本点的中心求出回归直线；将带入回归直线即可求出答案。

易错点

不知道回归直线过样本点的中心，误将表格中的点带入回归直线导致出错运算结果出错。

知识点

线性回归方程

1

题型：单选题

|

单选题 · 5 分

5．已知具有线性相关关系的两个变量之间的一组数据如下：

且回归直线方程为，根据模型预报当时，的预测值为（　　）

A

B

C

D

正确答案

C

解析

由题意可得，，，因为回归直线一定过样本点的中心，所以，解得．当时，的预测值为．故选D．

考查方向

本题主要考查线性回归直线方程、预测值等知识，意在考查考生处理数据和运算求解能力。

解题思路

1.先求出样本点的中心；2.然后带入求出回归直线后令即可得到答案。

易错点

1.不理解回归直线部分的基础知识，导致不知道该干什么；2.数据计算出错。

知识点

两个变量的线性相关线性回归方程

1

题型：简答题

|

简答题 · 13 分

随着我国经济的发展，居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款（年底余额）如下表：

（本小题满分13分，（Ⅰ）小问10分，（Ⅱ）小问3分）

18.求y关于t的回归方程

19.用所求回归方程预测该地区2015年（）的人民币储蓄存款.

附：回归方程中

第(1)小题正确答案及相关解析

正确答案

（Ⅰ）.

解析

试题分析：（Ⅰ）列表分别计算出，的值，然后代入求得，再代入求出值，从而就可得到回归方程．

试题解析：（1）列表计算如下

这里

又

从而.

故所求回归方程为.

考查方向

本题考查线性回归方程.

解题思路

本题考查线性回归直线方程的求法及应用，采用列表方式分别求出，的值然后代入给出的公式中进行求解.

易错点

准确运用公式求解有关量.

第(2)小题正确答案及相关解析

正确答案

（Ⅱ）千亿元.

解析

试题分析：（Ⅱ）将代入回归方程可预测该地区2015年的人民币储蓄存款．

试题解析：（2）将代入回归方程可预测该地区2015年的人民币储蓄存款为

考查方向

本题考查线性回归方程的具体应用

解题思路

本题考查线性回归直线方程的应用，代入数据求解即可.

易错点

注意运算的准确性.

1

题型：填空题

|

填空题 · 5 分

13.给出下列命题：

①线性相关系数r越大，两个变量的线性相关性越强；反之，线性相关性越弱；

②由变量x和y的数据得到其回归直线方程L:y =bx + a，则L一定经过点P(x,y)

③从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；

④在回归分析模型中，残差平方和越小，说明模型的拟合效果越好；

⑤在回归直线方程y = 0.lx + 10中，当解释变量x每增加一个单位时，预报变量y增加0.1 个单位，

其中真命题的序号是 .

正确答案

②④⑤

解析

①线性相关系数|r|越大，两个变量的线性相关性越强，故①不正确；

②由变量x和y的数据得到其回归直线方程l：y=bx+a，则l一定经过点P故②正确；

③从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样不是分层抽样，故③不正确；

④可用残差平方和判断模型的拟合效果，残差平方和越小，模型的拟合效果越好，故④正确；

⑤在回归直线方程y=0.1x+10中，当解释变量x每增加一个单位时，预报变量平均增加0.1个单位，故⑤正确．

故答案为：②④⑤

考查方向

本题线性相关、回归直线方程和拟合等相关概念。

易错点

对上述概念理解的不透彻

知识点

命题的真假判断与应用分层抽样方法线性回归方程相关系数

1

题型：单选题

|

单选题 · 5 分

5.某产品在某零售摊位的零售价x（单位：元）与每天的销售量y（单位：个）的统计资料如下表所示：

由此表可得回归直线方程，据此模型预测零售价为5元时，每天的销售量为（）

A23个

B24个

C25个

D26个

正确答案

B

解析

，代入回归方程得：，，，A、C、D选项不对，所以选B选项。

考查方向

本题主要考查了回归直线方程/在高考中不经常考查，主要考查用回归方程预测、样本中心、散点图。

解题思路

易错点

忽视回归直线经过样本中心，而用公式去求

知识点

线性回归方程

1

题型：简答题

|

简答题 · 12 分

19. 某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响，对近8年的宣传费和年销售量数据作了初步处理，得到下面的散点图及一些统计量的值。

（1）根据散点图判断，与，哪一个适宜作为年销售量y关于年宣传费x的回归方程类型（给出判断即可，不必说明理由）；

（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；

（3）已知这种产品的年利润z与x，y的关系为，根据（2）的结果回答下列问题：

（i）当年宣传费=49时，年销售量及年利润的预报值时多少？

（ii）当年宣传费为何值时，年利润的预报值最大？

正确答案

（1）由散点图可以判断，y=c+d适宜作为年销售量y关于年宣传费的回归方程式类型

（2）令，先建立y关于w的线性回归方程式。

由于,

，

所以y关于w的线性回归方程为,因此y关于的回归方程为

（3）由（2）知，当=49时，年销售量y的预报值

，

年利润z的预报值

根据（2）的结果知，年利润z的预报值

所以当，即=46.24时，取得最大值.

故年宣传费为46.24千元时，年利润的预报值最大.

解析

解析已在路上飞奔，马上就到！

知识点

散点图线性回归方程

热门试卷

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点