- 数列与其它知识的综合问题
- 共8题
1
题型:简答题
|
17.等差数列{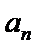
(I)求{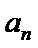
(II)设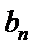
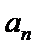
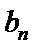
正确答案
知识点
等差数列的前n项和及其最值其它方法求和数列与其它知识的综合问题
1
题型:填空题
|
等差数列{
(I)求{
(II)设


正确答案
(Ⅰ)设数列


所以

(Ⅱ)由(Ⅰ)知
当n=1,2,3时,
当n=4,5时,
当n=6,7,8时,
当n=9,10时,
所以数列

知识点
等差数列的性质及应用其它方法求和数列与不等式的综合数列与其它知识的综合问题
1
题型:简答题
|
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
对于无穷数列{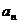
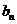
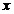
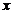
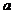


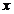
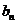
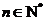
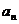
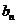
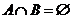
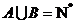
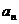
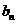
(1)若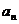
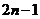
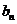
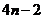
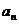
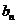
(2)若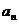
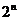
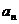
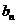
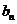
(3)若{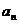
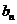
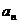
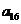
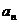
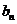
正确答案
(1)因为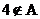
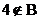

从而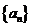
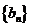
(2)因为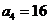
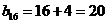
数列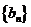
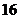
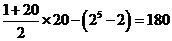
(3)设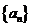
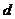
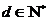
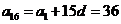
由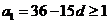
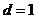
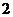
若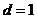
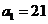
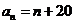
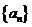
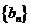
若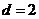
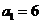
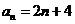
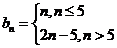
综上,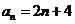
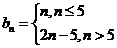
知识点
其它方法求和数列与函数的综合数列与其它知识的综合问题
已完结
扫码查看完整答案与解析