求函数y＝Asin(ωx＋φ)的解析式
共127题

· 求函数y＝Asin(ωx＋φ)的解析式

求函数y＝Asin(ωx＋φ)的解析式
共127题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

20．已知向量，．函数．

（1）若，求的值；

（2）在中，角的对边分别是，且满足，求的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

填空题 · 4 分

10．解方程

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

简答题 · 12 分

18．如图所示，四棱锥P－ABCD的底面是边长为1的正方形，PA⊥CD，PA = 1， PD＝，E为PD上一点，PE = 2ED．

（Ⅰ）求证：PA 平面ABCD；

（Ⅱ）求二面角D－AC－E的余弦值；

（Ⅲ）在侧棱PC上是否存在一点F，使得BF // 平面AEC？若存在，指出F点的位置，并证明；若不存在，说明理由．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

单选题 · 5 分

3．函数在定义域A上的值域为，则区间A不可能为（）

A[0,4]

B[2,4]

C[1,4]

D[-3,1]

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

简答题 · 14 分

22.已知椭圆的上顶点为，右焦点为，为等腰直角三角形（为坐标原点），抛物线的焦点恰好是该椭圆的右顶点。

（1）求椭圆的方程；

（2）若点分别是椭圆的下顶点和上顶点，点是椭圆上异与的点，求证：直线和直线的斜率之积为定值。

（3）已知圆的切线与椭圆相交于两点，那么以为直径的圆是否经过定点？如果是，求出定点的坐标；如果不是，请说明理由。

正确答案

（1）

（2）

（3）

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

填空题 · 4 分

16．关于函数（，有下列命题：

① 的图象关于直线对称

② 的图象可由的图象向右平移个单位得到

③ 的图象关于点（对称

④ 在上单调递增

⑤ 若可得必为的整数倍

⑥ 的表达式可改写成

其中正确命题的序号有（）

正确答案

①④

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

简答题 · 12 分

16．已知集合。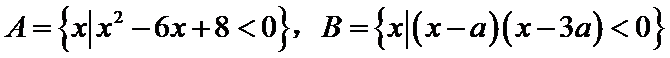

（1）若的充分条件，求的取值范围；

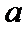
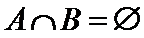
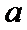
（2）若，求的取值范围。

正确答案

（1）当a=0时，B=∅，不合题意．

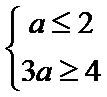
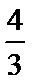
当a＞0时，B={x|a＜x＜3a}，要满足题意，则，解得≤a≤2．

当a＜0时，B={x|3a＜x＜a}，要满足题意，则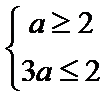，a∈∅．

综上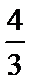，≤a≤2；

（2）要满足A∩B=∅，当a＞0时，B={x|a＜x＜3a}，

则a≥4或3a≤2，即0＜a≤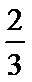或a≥4；

当a＜0时，B={x|3a＜x＜a}，则a≤2或a≥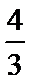，即a＜0；

当a=0时，B=∅，A∩B=∅．综上所述，a≤或a≥4．

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

单选题 · 5 分

5．已知直线与圆相交于两点，且则的值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

单选题 · 5 分

5．已知f（x）＝ax2＋bx是定义在[a－1,2a]上的偶函数，那么a＋b的值是（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

单选题 · 5 分

5．，下列不等式中一定成立的是（）

A若，则

B若，则

C若，则

D若，则

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

继续学习学习下一知识点

下一知识点 : 函数y＝Asin(ωx＋φ)的应用

百度题库 > 高考 > 文科数学 > 求函数y＝Asin(ωx＋φ)的解析式

扫码查看完整答案与解析