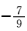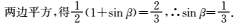求函数y＝Asin(ωx＋φ)的解析式
共127题

· 求函数y＝Asin(ωx＋φ)的解析式

求函数y＝Asin(ωx＋φ)的解析式
共127题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

6．已知抛物线的焦点与双曲线的一个焦点重合，则该双曲线的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

简答题 · 12 分

16．某学生社团在对本校学生学习方法开展问卷调查的过程中发现，在回收上来的1000份有效问卷中，同学们背英语单词的时间安排共有两种：白天背和晚上睡前背。为了研究背单词时间安排对记忆效果的影响，该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样，并完成一项实验．实验方法是，使两组学生记忆40个无意义音节（如XIQ、GEH），均要求在刚能全部记清时就停止识记，并在8小时后进行记忆检测。不同的是，甲组同学识记结束后一直不睡觉，8小时后测验；乙组同学识记停止后立刻睡觉，8小时后叫醒测验．

两组同学识记停止8小时后的准确回忆（保持）情况如图（区间含左端点而不含右端点）．

（1）估计这1000名被调查学生中停止后8小时40个音节的保持率不小于60%的人数；

（2）从乙组准确回忆单词个数在个范围内的学生中随机选2人，求能准确回忆个单词至少有一人的概率。

正确答案

总共抽取了人，由甲组的条形图可知甲组有有：4+10+8+4+2+1+1=30人；故乙组有20人

乙组的频率为：即有1+1+2+2+6+5+3=20人。

因为按5%的比例对这1000名学生按时间安排类型进行分层抽样

所以“白天背”的同学共有人，“晚上睡前背”的同学有400人。

（1）40个音节的保持率不小于60%,则至少能准确回忆24个，

“白天背”的同学共有人，“晚上睡前背”的同学有人。

所以这1000名被调查学生中停止后8小时40个音节的保持率不小于60%的人数大约为180人

（2）乙组准确回忆单词个数在个范围内的学生有6人，能准确回忆个单词的学生有2人。

从6人中随机抽取2人，用列举法可得有15种可能结果

法一、两人都能准确回忆个单词的可能结果有6种，故所求概率为：

法二、至少有一人能准确回忆个单词的可能结果有种，故所求概率为：

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

填空题 · 5 分

14．如图，在ABC中，点E在AB边上，点F在AC边上，且，BF与CE交于点M，设，则的值为_______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

填空题 · 5 分

7．已知则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

单选题 · 5 分

4.已知函数f(x)= ，若x0是y=f(x)的零点，且0<t<x0，则f(t)（）

A恒小于0

B恒大于0

C等于0

D不大于0

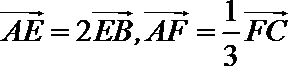
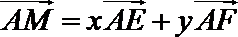
正确答案

解析

当x>0时，由f(x)=( )x-log2x=0，得()x=log2x，

在同一坐标系中分别作出y=( )x，y=log2x的图象(图略)，

由图象可知，当0<t<x0时，( )t>log2t，

所以此时f(t)恒大于0.

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

简答题 · 12 分

20．已知函数．

（1）求函数的单调增区间；

（2）若函数在上的最小值为，求实数的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

填空题 · 5 分

16. 如图，在二面角内半径为1的圆与半径为2的圆分别在半平面、内，且与棱切于同一点P，则以圆与圆为截面的球的表面积等于_____________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

单选题 · 5 分

5.要做一个圆锥形的漏斗，其母线长为20 cm，要使其体积最大，则其高为（）

Acm

B100 cm

C20 cm

Dcm

正确答案

解析

设圆锥的高为h，底面半径为r，体积为V

则V=πr2h=π(202-h2)h=-πh3+h

∴V'=-πh2+.

令V'=-πh2+=0,解得h=

当0<h<时，V'>0

当h>时，V'<0

∴当h=时，V最大.

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

单选题 · 5 分

1.已知，则sin β的值为（）

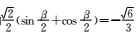
正确答案

解析

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

单选题 · 5 分

2.MN是过抛物线x2=2py的焦点的动弦，直线l1，l2是抛物线两条分别切于M，N的切线，且交于点P(0，- 1)，则p=（）

正确答案

解析

找特殊情况，当MN⊥y轴时，MN的方程为y=，与抛物线方程联立得x=±p，

不妨设M( -p，)，N(p，).

因为y=，所以y'=，

所以过点M的斜率k=- =-1，

所以过点M的切线方程为y=-x－，

因为P在该切线上，所以-1=0－

解得p=2，故选B.

知识点

求函数y＝Asin(ωx＋φ)的解析式

继续学习学习下一知识点

下一知识点 : 函数y＝Asin(ωx＋φ)的应用

百度题库 > 高考 > 文科数学 > 求函数y＝Asin(ωx＋φ)的解析式

扫码查看完整答案与解析