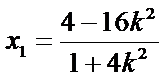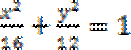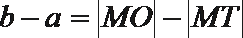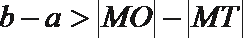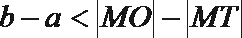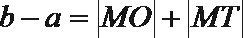- 直线、圆及圆锥曲线的交汇问题
- 共97题
12.已知圆C的圆心坐标为

正确答案
解析
.
根据抛物线几何性质可知准线方程

所以圆的标准方程为
考查方向
解题思路
该题思路比较清晰,主要有以下几个步骤1、写出准线方程


易错点
本题易错点主要集中在准线的表达,弦长公式的表达
知识点
10.双曲线

正确答案
解析
圆心坐标为


考查方向
本题主要考查了离心率的求解/本题主要考查运算求解能力
易错点
找不到关于a、b、c的方程,计算量大,容易出现计算错误。
知识点
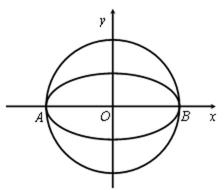
20.如图,椭圆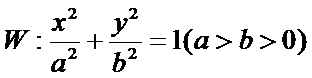
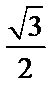
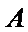
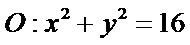
(Ⅰ)求椭圆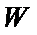
(Ⅱ)直线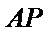
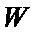
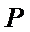

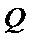
(i)当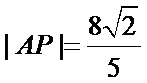
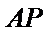
(ii)是否存在直线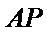
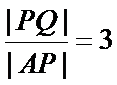
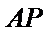
说明理由.
正确答案
(Ⅰ)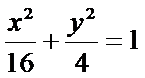
(Ⅱ)(i)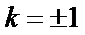
(ii)不存在直线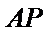
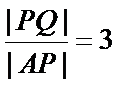
解析
(Ⅰ)
因为椭圆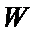

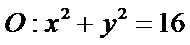
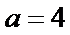
又离心率为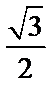
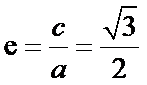
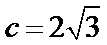
所以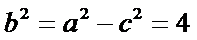
所以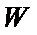
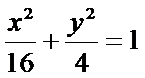
(Ⅱ)(i)
法一:设点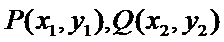
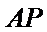
设直线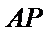
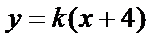
与椭圆方程联立得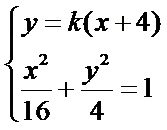
化简得到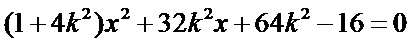
因为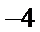

所以
由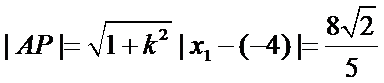
代入得到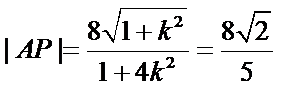
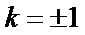
所以直线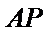
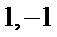
(ii)因为圆心到直线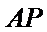
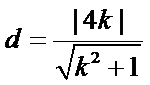
所以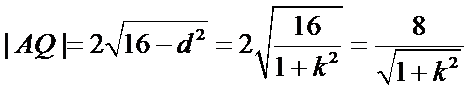
因为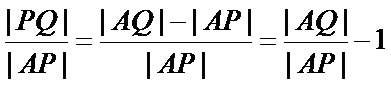
代入得到
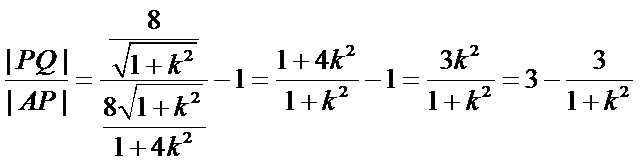
显然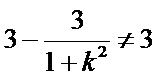
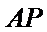
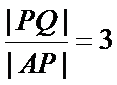
法二:(i)设点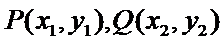
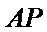
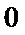
设直线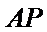
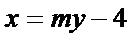
与椭圆方程联立得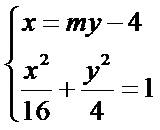
化简得到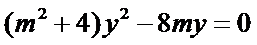
显然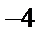
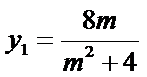
由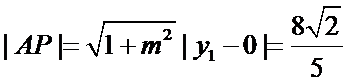
代入得到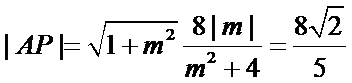
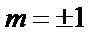
所以直线
(ii)因为圆心到直线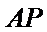
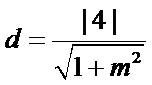
所以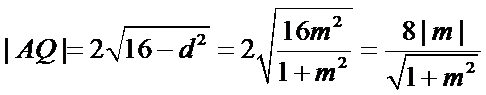
因为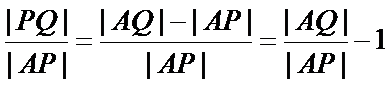
代入得到
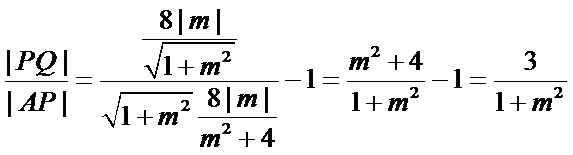
若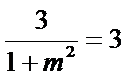
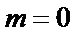
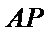
所以不存在直线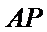
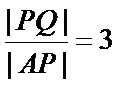
考查方向
本题考查了椭圆的综合求解能力,在近几年的各省高考题出现的频率较高.
解题思路
(Ⅰ)由椭圆的左顶点求出a,再有离心率求出c,进而求得b的值;
(Ⅱ)(i)联立方程,利用韦达定理求得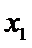
(ii)利用垂径定理求解.
易错点
计算量大,易出错.
知识点
20.已知椭圆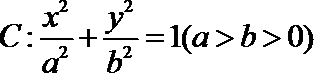
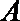
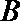
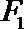
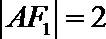
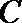
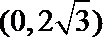
(Ⅰ)求椭圆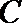
(Ⅱ)点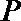
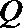
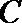
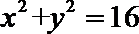
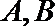
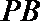
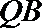
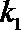
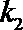
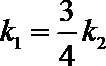
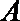
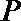
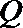
正确答案
(1)椭圆C的方程为
(2)见解析
解析
本题属于直线与椭圆关系的基本问题,题目的难度是逐渐由易到难,
(1)根据题目条件和a、b、c的关系可求
(2)设出两个交点的坐标
(3)根据已知条件,求出斜率关系,最后得出结论。
解:(I)由已知可得a-c=2,b=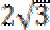
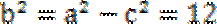
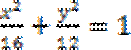
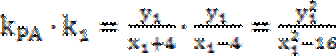
因为P(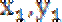
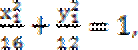
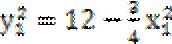
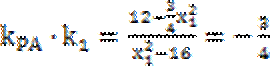
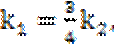
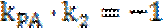
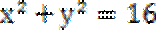
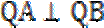
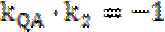
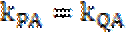
考查方向
本题考查了椭圆的基本性质以及直线与椭圆的位置关系等知识点,考查了学生分析问题与思考问题的能力,直线与圆锥曲线(特别是椭圆)的关系,是高考的重点内容,涉及的知识点较多,运算也比较复杂,对学生的运算能力有较高的要求,有时会与向量、距离、基本不等式、一元二次方程根与系数关系交汇在一起。
易错点
1、椭圆中a、b、c的关系会与双曲线中的搞错
2、第二问证三点共线,通常是证有公共点的两条直线的斜率相等(或者是采用向量的方法)
知识点
11.过双曲线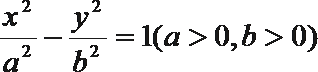
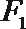
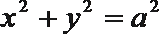
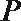
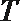
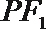
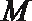
正确答案
解析
连结P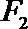
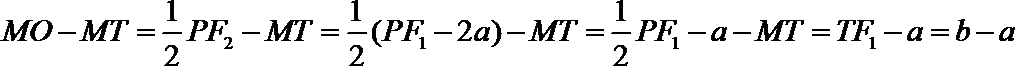
考查方向
本题考查学生的解析几何的综合运用的能力。
解题思路
将已知线段向焦半径转化,利用双曲线的性质解决。
易错点
1、不能正确地将已知条件进行转化;
2、解决综合问题的能力不强。
知识点
扫码查看完整答案与解析