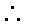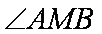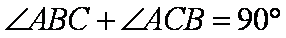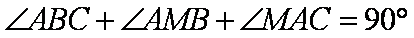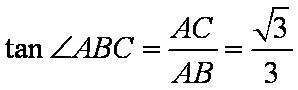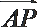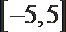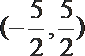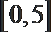- 弦切角
- 共14题
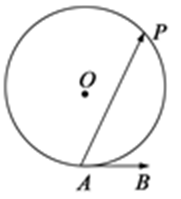
22. 如图5,圆O的直径
割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC
于点E,交直线AD于点F.
(Ⅰ) 当

(Ⅱ) 求
正确答案
(1)
解析
:(Ⅰ) 连结BC,∵AB是圆O的直径 ∴则
又



∵
(Ⅱ):由(Ⅰ)知
∴D、C、E、F四点共圆,---------------------------------6分
∴
∵PC、PA都是圆O的割线,∴
∴
考查方向
解题思路



易错点
不会使用第(1)问的结论推导第(2)问;
知识点
如图,已知⊙O中,直径AB垂直于弦CD,垂足为M,P是CD延长线上一点,PE切⊙O于点E,连接BE交CD于点F,证明:
(1)∠BFM=∠PEF;
(2)PF2=PD·PC.
正确答案
见解析
解析
(1)连接OE,
∵PE切⊙O于点E,∴OE⊥PE.
∴∠PEF+∠FEO=90°。
又∵AB⊥CD,
∴∠B+∠BFM=90°。
又∵∠B=∠FEO,
∴∠BFM=∠PEF.
(2)∵∠EFP=∠BFM,
∴∠EFP=∠PEF.
∴PE=PF.
又∵PE2=PD·PC,
∴PF2=PD·PC.
知识点
已知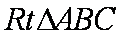
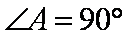
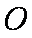
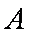
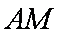
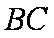
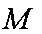
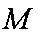
交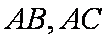
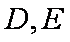
(1)求证: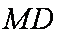
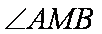
(2)若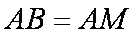
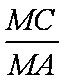

正确答案
见解析
解析
证明:(1)由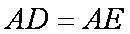

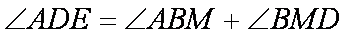
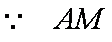
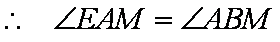

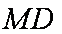
(2)由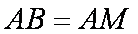
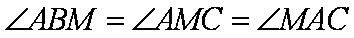
即
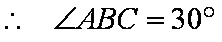
知识点
10.如图,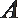
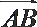
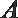
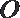
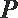
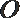
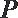
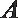
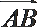
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析