热门试卷

∵平面垂直的判定定理：如果一个平面经过另一个平面的垂线，则两平面垂直

∴直线m⊂α，那么“m⊥β”成立时，一定有“α⊥β”成立

反之，直线m⊂α，若“α⊥β”不一定有“m⊥β”成立

所以直线m⊂α，那么“m⊥β”是“α⊥β”的充分不必要条件

故选A

∵平面垂直的判定定理：如果一个平面经过另一个平面的垂线，则两平面垂直

∴直线m⊂α，那么“m⊥β”成立时，一定有“α⊥β”成立

反之，直线m⊂α，若“α⊥β”不一定有“m⊥β”成立

所以直线m⊂α，那么“m⊥β”是“α⊥β”的充分不必要条件

当a=3时，两条直线的方程分别是3x+3y=0和2x+2y=3，此时两条直线平行成立

反之，当两条直线平行时，有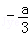=﹣1即a=3，

所以“a=3”是“直线ax+3y=0和2x+2y=3平行的”的充分必要条件。

∵“x ＞0”可得x＞1或﹣1＜x＜0，

若x＞1可得“x ＞0“，

∴“x＞1”⇒“x ＞0”，反之不成立。

∴“x＞1”是“x ＞0”的充分非必要条件。