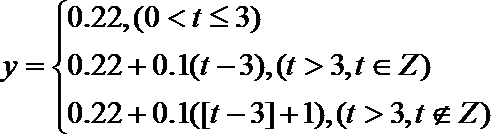- 设计程序框图解决实际问题
- 共46题
9.中国古代有计算多项式值得的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依闪输入的a为2,2,5,则输出的s=( )
正确答案
知识点
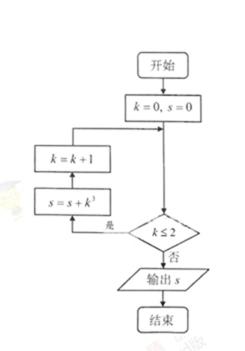
3.执行如图所示的程序框图,输出的s值为
正确答案
知识点
21.中国网通规定:拨打市内电话时,如果不超过3分钟,则收取话费0.22元;如果通话时间超过3分钟,则超出部分按每分钟0.1元收取通话费,不足一分钟按以一分钟计算。设通话时间为t(分钟),通话费用y(元),如何设计一个程序,计算通话的费用。
正确答案
算法分析:
数学模型实际上为:y关于t的分段函数。
关系是如下:
其中[t-3]表示取不大于t-3的整数部分。
算法步骤如下:
第一步:输入通话时间t;
第二步:如果t≤3,那么y = 0.22;否则判断t∈Z 是否成立,若成立执行y= 0.2+0.1× (t-3);否则执行y = 0.2+0.1×( [t-3]+1)。
第三步:输出通话费用c 。
算法程序如下:
INPUT “请输入通话时间:”;t
IF t<=3 THEN
y=0.22
ELSE
IF INT(t)=t THEN
y=0.22+0.1*(t-3)
ELSE
y=0.22+0.1*(INT(t-3)+1)
END IF
END IF
PRINT “通话费用为:”;y
END
解析
解析已在路上飞奔,马上就到!
知识点
4.根据下图所示的伪代码,可知输出的结果S为
正确答案
21
解析
【解析】模拟执行程序,开始有I=1,S=0,此时满足条件S≤10;接下来有I=2,S=1,此时满足条件S≤10;接下来有I=3,S=1+4=5,此时满足条件S≤
考查方向
解题思路
本题主要考查伪代码,阅读能力.简单的推理运算能力。解题步骤如下:
从I=1开始一直循环到I=4
退出循环,输出结果。
易错点
本题容易出错的地方就是循环的结束的确定。
知识点
6.执行如图所示的程序框图,若输出的结果为2,则可输入的实数x值的个数为( )
正确答案
解析
由



考查方向
本题主要考查了程序框图与分段函数的综合应用问题,为高考必考题,在近几年的各省高考题出现的频率较高,常与数列求和、分段函数等知识点交汇命题。
解题思路
根据判断框条件直接计算对数的值。
易错点
对循环条件的判断失误导致出错。
知识点
15.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为 .(参考数据:sin15°=0.2588,sin7.5°=0.1305)
正确答案
24
解析
当
当
当
所以输出n的值为24.
考查方向
解题思路
对每一次循环S的值进行计算,并与3.10进行比较,判断下一步是循环还是输出n的值。
易错点
本题易在计算S的值时发生错误。
知识点
扫码查看完整答案与解析