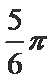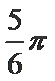- 三角函数的化简求值
- 共61题
17.设
正确答案
解析
考查方向
解题思路
三角函数值相等，考虑角的关系
易错点
讨论
知识点
17.设
（I）求
（II）把
正确答案
（
（
解析
试题分析：（
由
写出
（
试题解析：（
由
所以，
（或
（
把
得到
再把得到的图象向左平移
即
所以
考查方向
知识点
7．已知
A．
B．
C．
D．
正确答案
解析
因为
所以
考查方向
解题思路
直接化简求值。
易错点
不会将其转化为2倍角公式去化简。
知识点
13.函数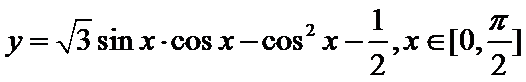
正确答案
解析
试题分析：依题意可知
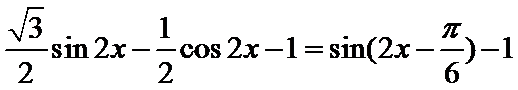
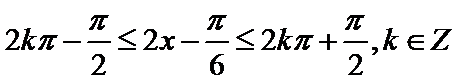
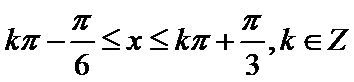
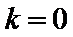
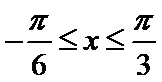
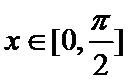
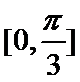
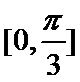
考查方向
解题思路
先化简函数解析式，再求单调区间。
易错点
化简函数解析式时因对三角恒等变换共识不熟悉导致出错。
知识点
13. 已知
正确答案
解析
考查方向
解题思路
先求出
易错点
计算错误,对公式定理掌握不好
知识点
6．若
A
B
C
D
正确答案
解析
考查方向
解题思路
本题考查角的变换及正切的差角公式，采用先将未知角
易错点
注意运算的准确性
知识点
14．若
正确答案
解析
∵
∴
∵
考查方向
本题主要考查了三角恒等变换
解题思路
先求出
易错点
本题找出角之间关系
知识点
9．化简：4sin40°-tan40°等于（ ）
A1
B
C
D2
正确答案
解析
试题分析：本题属于三角函数中的基本问题，题目的难度是逐渐由易到难。注意化简时对两角和差公式的选取．
考查方向
本题主要考查了三角函数的公式化简计算,在近几年的各省高考题出现的频率较高，常与三角恒等变形公式等知识点交汇命题。
解题思路
本题考查三角函数的公式化简计算，解题步骤如下：
由题可知，函数解析式化简为(2sin80°-sin40°)/cos40°=[2cos(40°-30°)-sin40°]/cos40°=
易错点
本题易在公式化简上发生错误。
知识点
9．已知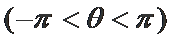
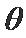
正确答案
解析
-(cos2x-sin2x)=-2cos(2x+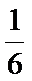
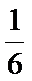
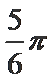
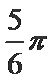
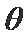
考查方向
解题思路
本题考查运用辅助角公式求辅助角，解题步骤如下：
先用辅助角公式得-2cos(2x+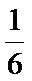
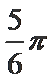
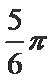
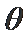
易错点
本题必须注意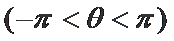
知识点
正确答案
知识点
扫码查看完整答案与解析