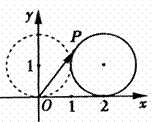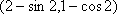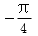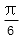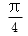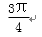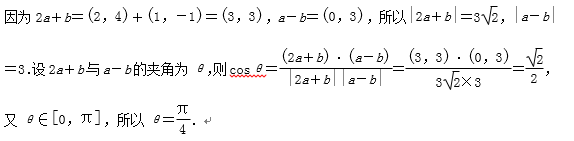平面向量坐标表示的应用
共7题

· 平面向量坐标表示的应用

平面向量坐标表示的应用
共7题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

8. 已知为的边的中点，所在平面内有一个点，满足，则的值为（）

正确答案

解析

根据中点是D，再结合向量加法的平行四边形法则可以得到D也是AP的中点故可以得等于1.

考查方向

向量的运算。

解题思路

根据中点是D，再结合向量加法的平行四边形法则可以得到D也是AP的中点故可以得到答案。

易错点

不会转化成所学内容。

知识点

向量的几何表示平面向量坐标表示的应用

题型：填空题

填空题 · 6 分

12．在边长为1的等边中，为直线上一点，若

，则， .

正确答案

，

解析

试题分析：由及P，B，C三点共线可得，解得，所以，故，故此题答案为，。

考查方向

本题主要考直线的向量参数方程及向量数量积的运算．

解题思路

直接运用三点共线的结论及向量的运算律进行计算。

易错点

忽视向量的夹角导致数量积求错。

知识点

向量的共线定理平面向量坐标表示的应用

题型：单选题

单选题 · 5 分

12．设A1，A2，A3，A4是平面直角坐标系中两两不同的四点，若＝λ（λ∈R），＝μ（μ∈R），且，则称A3，A4调和分割A1，A2，已知平面上的点C，D调和分割点A，B，则下面说法正确的是（　　）

AC可能是线段AB的中点

BD可能是线段AB的中点

CC、D可能同时在线段AB上

DC、D不可能同时在线段AB的延长线上

正确答案

解析

由已知，不妨设Ｃ（c,0）,D（d,0）,A（0,0）,B（1,0）,

由题意有（c，0）=λ（1，0），（d，0）=μ（1，0）

所以λ=c，μ=d，代入，得…（1）

若C是线段AB的中点，则c=，代入（1）

d不存在，故C不可能是线段AB的中点，A错误；

同理B错误；

若C，D同时在线段AB上，则，，代入（1）

得c=d=1，此时C和D点重合，与条件矛盾，故C错误．

故选：D．

知识点

命题的真假判断与应用平面向量坐标表示的应用

题型：填空题

填空题 · 4 分

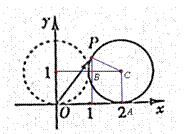
如图，在平面直角坐标系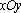中，一单位圆的圆心的初始位置在(0，1)，此时圆上一点P的位置在(0，0)，圆在x轴上沿正向滚动.当圆滚动到圆心位于(2，1)时，的坐标为＿＿＿＿.

正确答案

解析

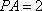
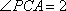
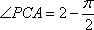
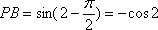
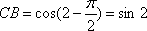
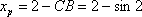
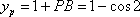
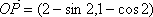
因为圆心移动的距离为2，所以劣弧，即圆心角, ,则,所以，，所以，，所以.

知识点

平面向量的坐标运算平面向量坐标表示的应用

题型：单选题

单选题 · 5 分

设，，，是平面直角坐标系中两两不同的四点，若 (λ∈R)，(μ∈R)，且,则称，调和分割， ,已知点C(c，o),D(d，O) (c，d∈R)调和分割点A(0，0)，B(1，0)，则下面说法正确的是

A可能是线段的中点

B可能是线段的中点

C可能同时在线段上

D不可能同时在线段的延长线上

正确答案

解析

由 (λ∈R)，(μ∈R)知:四点，，，在同一条直线上,

因为C,D调和分割点A,B,所以A,B,C,D四点在同一直线上,且, 故选D.

知识点

平面向量的坐标运算平面向量坐标表示的应用

题型：单选题

单选题 · 5 分

已知，，且，则

C或

正确答案

解析

略

知识点

平行向量与共线向量平面向量坐标表示的应用

题型：单选题

单选题 · 5 分

若向量a＝(1,2)，b＝(1，－1)，则2a＋b与a－b的夹角等于(　　)

正确答案

解析

知识点

平面向量坐标表示的应用数量积表示两个向量的夹角

已学完, 返回章节学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 文科数学 > 平面向量坐标表示的应用

扫码查看完整答案与解析