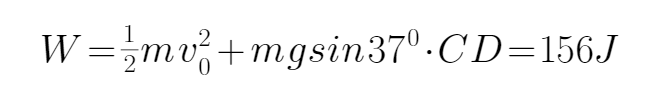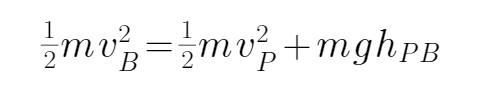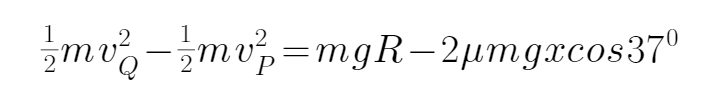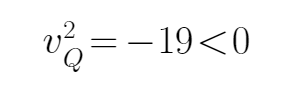- 功能关系
- 共276题
如图所示,光滑水平面上放有质量M=3kg和m=1kg可视为质点的小物块A.B,右端有质量m1=2kg,高h=1.2m的光滑弧形滑块C,下表面与水平面平滑接触,开始时三者静止。现使A.B间夹少许炸药,炸药爆炸,50%的化学能转化为A.B的机械能,B恰好能滑到弧形滑块最高点,g=10m/s2 ,求:
33.B滑到C的最高点时的速度大小;
34.炸药爆炸时释放的化学能。
正确答案
①2m/s (6分)
解析
①设B滑上C前的速度为v1,恰好能到达C的最高点,说明BC达到共同速度,设为v共;双方相对运动的过程中系统的水平方向上动量守恒.机械能守恒,有:
mv1=(m+M′)v共


两式联立解得:v1=6m/s,v共=2m/s
考查方向
动量守恒定律;功能关系
解题思路
B恰好能到达C的最高点,说明BC达到共同速度,双方相对运动的过程中系统的水平方向上动量守恒、机械能守恒,根据动量守恒定律以及机械能守恒定律列式求解.
易错点
关键正确分析物体的受力情况和运动情况,知道B到达C的最高点时,C的速度不为零.
教师点评
本题考查了动量守恒定律,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
正确答案
②48J(4分)
解析
②炸药爆炸时,A的速度为v2,A.B构成的系统动量守恒,有:
mv1-Mv2=0
解得:v2=2m/s
由题意得:E化=2(

考查方向
动量守恒定律;功能关系
解题思路
炸药爆炸时,A、B构成的系统动量守恒,根据动量守恒定律求出爆炸后A的速度,再根据能量守恒定律求解即可.
易错点
关键理解炸药爆炸后,系统中的能量转化关系.
教师点评
本题考查了动量守恒定律,在近几年的各省高考题出现的频率较高,常与动能定理、能量守恒定律等知识点交汇命题.
如图(甲)所示,一倾角为370的传送带以恒定速率运行。现将一质量m=2 kg的小物体以某一初速度放上传送带,物体相对地面的速度随时间变化的关系如图(乙)所示,取沿传送带向上为正方向,g=10m/s2,sin 370=0.6,cos370=0.8.求:
29. 物体与传送带间的动摩擦因数;
30. 0~10 s内物体机械能增量及因与传送带摩擦产生的热量Q.
正确答案
μ=
解析
由速度图象可知,物体在传送带上加速运动的加速度

由牛顿第二定律 μmgcosθ-mgsinθ=ma 2分
μ=
考查方向
牛顿第二定理的应用
解题思路
根据斜率求出加速度,由牛顿第二定律求解物体与传送带间的动摩擦因数.
易错点
本题一要读懂速度图象,根据图象分析物体的运动情况,求出位移和加速度,二要根据牛顿第二定律和功能关系求解相关的量,对于热量,要根据相对位移求解.
正确答案
Q=252 J
解析
由速度图象可知,物体在0~10s内的位移

物体上升的高度h=Ssinθ 1分
增加的重力势能 △Ep=mgh=264J 2分
增加的动能 △Ek=
机械能变化量 △E=△Ep+ △Ek =276J 2分
0-10s内只有前6s内发生相对滑动.
在0-6s内传送带运动的距离为:s带=v带t=4×6m=24m,
物体的位移为:s物=6m
则物体与传送带的相对位移大小为:△s=s带-s物=24-6=18m
产生的热量为:Q=μmgcosθ•△s=0.875×2×10×0.8×18=252 J.
考查方向
功能关系 能量守恒定律.
解题思路
速度图象的“面积”大小等于位移,物体在0-2s内的位移为负值,在2-10s内的位移为正值.0-10s内物体机械能增量等于动能增加量与重力势能增加量之和.在前6s内物体与传送带发生相对滑动,求出相对位移△s,产生的热量为Q=μmgcosθ•△s.
易错点
本题一要读懂速度图象,根据图象分析物体的运动情况,求出位移和加速度,二要根据牛顿第二定律和功能关系求解相关的量,对于热量,要根据相对位移求解.
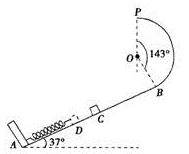
如图所示,AB为倾角θ=37°的斜面轨道,轨道的AC部分光滑,CB部分粗糙,BP为圆心角等于143°、半径R=l m的竖直光滑圆弧形轨道,两轨道相切于B点,P、O两点在同一竖直线上,轻弹簧一端固定在A点,另一自由端在斜面上C点处,现有一质量m
=2 kg的小物块在外力作用下将弹簧缓慢压缩到D点后(不栓接)释放,物块经过C点后,从C点运动到B点过程中的位移与时间的关系为x= 12t - 4t2(式中x单位是m,t单位是s),假设物块第一次经过B点后恰能到达P点,sin 37°=0.6,cos37°=0.8,g取10m/s2.试求:
14.若CD =1 m,试求物块从D点运动到C点的过程中,弹簧对物块所做的功;
15.B、C两点间的距离x;
16.若在P处安装一个竖直弹性挡板,小物块与挡板碰撞后速度反向,速度大小不变,小物块与弹簧相互作用不损失机械能,试通过计算判断物块在第一次与挡板碰撞后的运动过程
中是否会脱离轨道?
正确答案
156 J
解析
由x=12t-4t2知,物块在C点速度为:v0=12 m/s,
设物块从D点运动到C点的过程中,弹簧对物块所做的功为W,由动能定理得: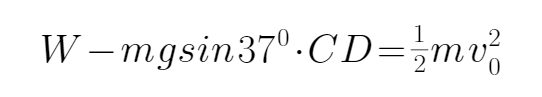
考查方向
动能定理
解题思路
物块从C点运动到B点过程中的位移与时间的关系x=12t-5t2,根据待定系数法可以判断出初速度和加速度的值.对物体运用动能定理求弹簧对物块所做的功.
易错点
掌握动能定理的应用.
正确答案
6.125m
解析
由x=12t-4t2知,物块从C运动到B的加速度大小为:a=8 m/s2,物块在P点的速度满足: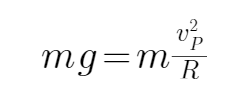
物块从C运动到B的过程中有:
由以上各式解得:x=6.125m
考查方向
机械能守恒定律; 匀变速直线运动的公式
解题思路
根据CB段匀减速直线运动的位移时间关系得出物体运动的加速度,从而根据牛顿第二定律求出动摩擦因数,因为物体恰好到达P点,根据牛顿第二定律得出P点的速度,通过机械能守恒定律得出B点的速度,然后通过匀变速直线运动的速度位移公式求出B、C两点间的距离xBC.
易错点
理解物块恰能到达P点的的临界条件.
正确答案
物块在以后的运动过程中不会脱离轨道.
解析
设物块与斜面间的动摩擦因数为μ,由牛顿第二定律得
mgsin θ+μmgcos θ=ma
代入数据解得μ=0.25
假设物块第一
解得
可见物块返回后不能到达Q点,故物块在以后的运动过程中不会脱离轨道.
考查方向
牛顿第二定律;动能定理
解题思路
根据动能定理判断物体能否返回时回到与O点等高的位置,若不能回到等高的位置,则小球将不会脱离轨道.
易错点
关键分析出物体在运动过程中在哪点最容易脱离轨道.
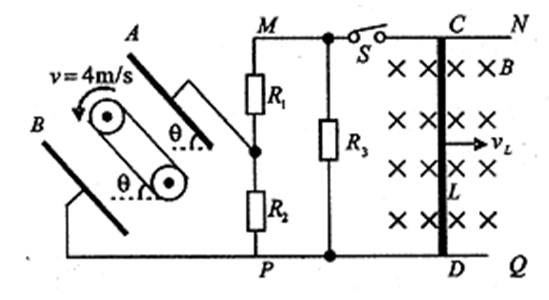
如图所示,足够长的导轨MN、PQ分别水平放置且位于同一竖直平面内,其间有垂直导轨平面水平向里的匀强磁场,磁感应强度为B=4T,长度为L=4m、电阻为r=lΩ的导体棒CD垂直导轨放置,在外力作用下,导轨以vL=4. 5m/s的速度水平向右匀速运动,电阻R1 =4Ω,R2=12Ω,R3=16Ω电容为C=0.2μF的平行板电容器的两极板A、B与水平面的夹角θ=37°,两极板A、B间的距离d= 0.4m,板间有一个传动装置,绝缘传送带与极板平行,皮带传动装置两轮轴心相距L= 5m,传送带逆时针匀速转动,其速度v=4m/s.现有一个质量m=0. lkg、电荷量q=+0. 02C的工件(视为质点,电荷量保持不变)轻放在传送带底端,同时开关
S闭合,电路瞬间能稳定下来,不计其余电阻,工件与传送带间的动摩擦因数为μ=0. 25,g=
10m/s2,sin37°= 0.6,cos37°=0.8.求:
14.开关S闭合后,电容器所带电量.
15.工件从传送带底端运动到顶端过程中
因摩擦所产生的热量.
正确答案
Q=9.6×10-6C
解析
E=BLVL=72V;U出=R外●E/R总=64V;
所以UAB=U出●R2/(R1+R2)=48V;
所以Q=CUAB=9.6×10-6C
考查方向
闭合电路欧姆定律以及电容器的电容。
解题思路
根据闭合电路欧姆定律求出电容器两端电压,再根据电容定义式求解。
易错点
输出电压与电源电动势的区别
教师点评
本问考察内容比较难,属于中难题。
正确答案
FN=mgcos37°+UABq/d=3.2N
f=μFN=0.8N
a=(f-mgsin37°)/m=2m/s2
t=2S
Δx=4m
Q=f●Δx=3.2J
解析
FN=mgcos37°+UABq/d=3.2N
f=μFN=0.8N
a=(f-mgsin37°)/m=2m/s2
t=2S
Δx=4m
Q=f●Δx=3.2J
考查方向
受力分析以及摩擦生热的计算
解题思路
先求正压力,即支持力,求出摩擦进而求出合外力,通过牛二求出加速度,速度,位移差,最终求摩擦生热
易错点
摩擦力做功与摩擦生热区别
教师点评
本题考察属于难题,受力分析在电容器中,容易分析错。
6.如图所示,某一空间内充满竖直向下的匀强电场E,在竖直平面内建立坐标xOy,在y<0的空间里有与场强E垂直的匀强磁场B,在y>0的空间内,将一质量为m的带电液滴(可视为质点)自由释放,此液滴则沿y轴的负方向以加速度a=2g(g为重力加速度)做匀加速直线运动,当液滴运动到坐标原点时,瞬间被安置在原点的一个装置改变了带电性质(液滴所带电荷量和质量均不变),随后液滴进入y<0的空间运动。

正确答案
解析
A、带电粒子在电场与重力场作用下,由牛顿第二定律可得:qE+mg=ma=m•2g,故qE=mg
当带电粒子进入磁场时,由于电场力与重力方向相反,处于平衡.而洛伦兹力提供向心力,做匀速圆周运动.
所以重力势能先减小后增大,故A正确;
B、由于电场力先作负功后做正功,所以电势能先增大后减小,那么机械能先减小后增大,故B错误;
CD、由于做匀速圆周运动,则速度的大小不变,则动能不变,故C错误,D正确;
故选:AD.
考查方向
带电粒子在混合场中的运动
解题思路
带电粒子仅在电场与重力场作用下,做匀加速直线运动.根据牛顿第二定律可知,电场力与重力的关系;当进入磁场前,由于电性的改变,导致电场力与重力平衡,从而仅由洛伦兹力提供向心力,使其做匀速圆周运动,因此即可求解.
易错点
带电粒子在不同场的受力分析,并根据牛顿第二定律来确定其运动状态.
知识点
扫码查看完整答案与解析