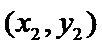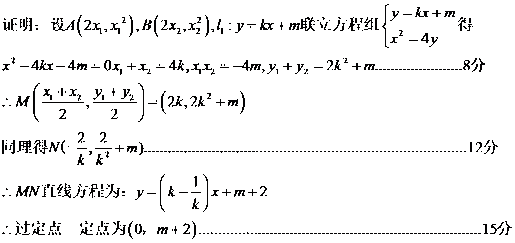抛物线的有关应用
共18题

· 抛物线的有关应用

抛物线的有关应用
共18题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

20.在直角坐标系中，直线l:y=t(t≠0)交y轴于点M，交抛物线C：于点P，M关于点P的对称点为N，连结ON并延长交C于点H.

（I）求；

（II）除H以外，直线MH与C是否有其它公共点？说明理由.

正确答案

解：将直线l与抛物线联立∴ 解得

(1) ∵ M关于P的对称点为N ∴ ∴ 即

∴ ON直线斜率 ∴ ON方程

则H点坐标∴解答 ∴

∴‍=2

(2)由①知∴ MH直线程

与抛物线联立得

即y2-4ty=4t2 ∴∴直线MH与抛物相切

∴ 直线MH与曲线C除点H外没有其它公共点

知识点

抛物线的定义及应用抛物线焦点弦的性质抛物线的有关应用

题型：单选题

单选题 · 5 分

6.已知点及抛物线上一动点，则的最小值是（）

正确答案

解析

如图：注意点Q的位置

根据题意得知

选C

考查方向

本题重点考察了抛物线的标准方程和几何性质，考察了抛物线焦点弦的性质，考察了不等式的应用，借助于数形结合，该题属于简单题

解题思路

1）把转化为点Q到准线的距离问题，

2）利用不等式的性质直接得出结果

易错点

主要易错于的转换

知识点

抛物线的标准方程和几何性质抛物线的有关应用

题型：填空题

填空题 · 4 分

14．已知则等于_________________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的有关应用

题型：单选题

单选题 · 5 分

15．下列函数中，与函数的值域相同的函数为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的有关应用

题型：单选题

单选题 · 5 分

9．用C(A)表示非空集合A中的元素个数，定义A*B=。若A={1,2}B=，且A*B=1，设实数的所有可能取值集合是S，则C(S)=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的有关应用

题型：单选题

单选题 · 5 分

12．已知抛物线的焦点为，、为抛物线上两点，若，为坐标原点，则△的面积为( )

正确答案

解析

抛物线的焦点为（1，0）

设直线的方程为：,

代入抛物线方程可得

设,则

由AF=3FB，得,则，

故选C

考查方向

抛物线的性质，直线和抛物线的结合问题

解题思路

先表示出来三角形AOB的面积公式，然后求出相应的三角形的边长

易错点

计算能力弱

知识点

抛物线的有关应用

题型：填空题

填空题 · 5 分

16.已知抛物线的焦点为，动点在上，圆的半径为，过点的直线与圆切于点，则的最小值为．

正确答案

解析

由题意可知，由抛物线的定义可知：,d为点Q到准线的距离，易知，抛物线的顶点到准线的距离最短，

考查方向

抛物线的几何性质，抛物线与直线的结合题

解题思路

根据抛物线的定义，够造出FQ的表达式，然后求出最小值

易错点

计算错误，圆锥曲线性质掌握不好

知识点

抛物线的有关应用

题型：简答题

简答题 · 15 分

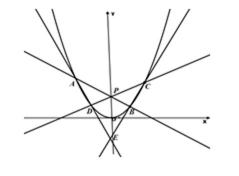
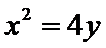
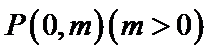
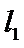
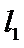
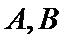
如图，过抛物线的对称轴上一点作直线，与抛物线交于两点.

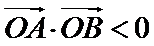
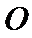
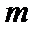
22.若(为坐标原点)，求实数的取值范围；

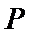
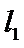
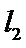
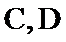
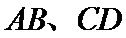
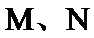
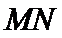
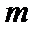
23.过点且与垂直的直线与抛物线交于两点, 设的中点分别为求证：直线必过定点,并求出该定点坐标（用表示）.

第(1)小题正确答案及相关解析

正确答案

详见解析

解析

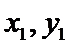
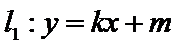
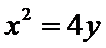
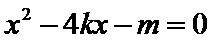
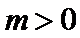
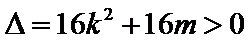
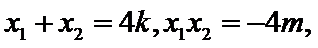
解：设 A()．B代入抛物线的方程化简得

………………………………………………………………….…2分

∵ ∴恒成立

……………………………………………………………………………………..4分

因为，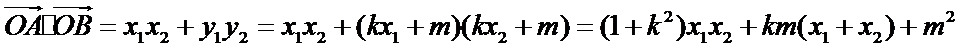

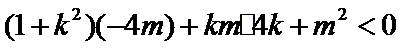
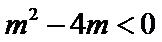
则，即，……………………6分

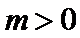
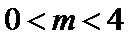
又因为，解得……………………………………………….7分

考查方向

抛物线的简单性质与应用

解题思路

设l1：y=kx+m，与抛物线方程联立方程组消元，根据根与系数的关系计算

易错点

计算能力弱

第(2)小题正确答案及相关解析

正确答案

详见解析

解析

考查方向

抛物线的简单性质

直线与圆锥曲线的综合题

解题思路

由（I）中的方程组得出x1+x2，y1+y2，得出AB的中点M的坐标，同理得出CD的中点N的坐标，得出MN的直线方程，化为斜截式方程得出定点坐标．

易错点

对直线与圆锥曲线的位置关系掌握不好，计算能力弱

已学完, 返回章节学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 文科数学 > 抛物线的有关应用

扫码查看完整答案与解析