- 线面角和二面角的求法
- 共51题
如图,已知





19.求证:EF∥平面
20.求证:平面

21.求直线

正确答案
要证明EF∥平面

证明:如图,连接





解析
见答案.
考查方向
易错点
线面关系与面面关系的转化
正确答案
要证明平面



因为AB=AC,E为BC中点,所以










解析
见答案.
考查方向
易错点
线面垂直于面面垂直的转化.
正确答案

解析
取









取

























考查方向
易错点
线面角定义的灵活运用
19. 如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
(I)证明:
(II)若
正确答案
(Ⅰ)证明详见解析;(Ⅱ)
解析
(Ⅰ)证





试题解析:(I)由已知得,
又由

由此得

(II)由
由
所以
于是
由(I)知

所以

又由

又由
五边形
所以五棱锥
考查方向
解题思路
(Ⅰ)先证








易错点
第一问证那两条线垂直。立体几何中的折叠问题,应注意折叠前后线段的长度、垂直关系哪些变了,哪些没变.
知识点
11.平面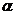
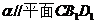
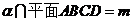
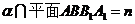
正确答案
知识点
考生在第22、23、24题中任选一道作答,并用2B铅笔将答题卡上所选的题目对应的题号右侧方框涂黑,按所涂题号进行评分;多涂、多答,按所涂的首题进行评分.
22.【选修4—1】几何证明选讲(请回答27、28题)
如图,在






23.【选修4—4】极坐标与参数方程(请回答29、30题)
在直角坐标系







24.【选修4—5】不等式选讲(请回答31、32题)
已知
27.求证:
28.求线段
29.化

30.若








31.求不等式
32.设


正确答案
证明:由已知




解析
(Ⅰ)证明:由已知




考查方向
解题思路
由割线定理求解。
易错点
不会利用切割线定理来解答。。
正确答案

解析
(Ⅱ)解:如图,过点






同理

①+②得
即
所以


考查方向
解题思路
由割线定理求解。
易错点
不记得定理。
正确答案
(Ⅰ)







解析
(Ⅰ)







考查方向
解题思路
参数方程化为普通方程。
易错点
极坐标转不会化为直角坐标,参数方程不会转化为普通方程。
正确答案
解析
(Ⅱ)当

设





从而当

考查方向
解题思路
极坐标方程化为直角坐标中的方程再利用点到直线的距离公式再结合三角函数即可。
易错点
不知道参数的几何意义。
正确答案
解析
(Ⅰ)解:不等式


所以不等式
考查方向
解题思路
去掉绝对值分类讨论求解。
易错点
不会去掉绝对值。
正确答案
因为
因为


同理:

所以
所以
解析
证明:因为
因为


同理:

所以
所以
考查方向
解题思路
利用基本不等式来解决.
易错点
不会利用基本不等式处理。。
如图所示的几何体是由以正







20.求证:直线

21.求直线

正确答案
见解析
解析
(1)证:取DE的中点G,连结GF.由三棱柱得,AF//BD//CE,
∵OG为梯
而CE//AF,且AF=2 ∴OG
∴四边形OAFG为平行四边形 ∴GF//OA
又OA

考查方向
解题思路
该题解题关键在于找到所求内容的突破点
取DE的中点G,连结GF.由三棱柱得,AF//BD//CE,得到OG为梯
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错
正确答案
见解析
解析
(2)∵

又
在面BCED中,过C作
∴
在ΔCFH中,


∴直线FC和面DEF所成角的正弦值为
注:解法2可用等积法;解法3可用空间直角坐标系
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
通过在面BCED中,过C作


易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错
20.如图,在四棱锥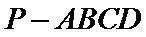


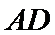

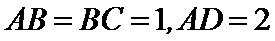
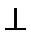


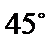

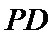
(Ⅰ)求证: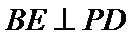
(Ⅱ)求二面角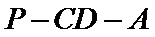
正确答案
解:
解法二:(1) 如图,建立空间直角坐标系,由已知可得:余弦
A(0,0,0), B(1,0,0),C(1,1,0),
D(0,2,0), P(0,0,2), E(0,1,1),
(2)
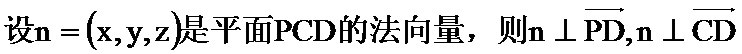
由
得
令y=1,则n=(1,1,1),
所以,所求二面角的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
6.在长方体






正确答案
解析
如图,过









知识点
16.关于正四棱锥
①异面直线
②侧面为锐角三角形;
③侧面与底面所成的二面角大于侧棱与底面所成的角;
④相邻两侧面所成的二面角为钝角;
其中正确的命题序号是___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,E为AD上一点,F为PC上一点,四边形BCDE为矩形,∠PAD=60°,PB=2√3,PA=ED=2AE=2.(1)若




正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)连接



因为



所以
因为

因为

所以
(2)因为
所以
所以
又平面





(3)由(2)知,
∴ ∠PBE为直线PB与平面ABCD所成的角,
在RtΔPEB中,


直线PB与平面ABCD所成的角为60°.
考查方向
解题思路
本题考查立体几何中的线面位置关系,解题步骤如下:1、利用线面平行的性质定理。2、利用线面垂直的定义及判定定理转化。
易错点
1、第一问中的线线平行的判定。2、第二问中求证线面垂直时要与平面内的两条相交直线垂直。
知识点
正确答案
知识点
扫码查看完整答案与解析