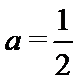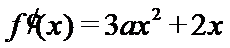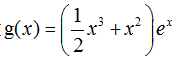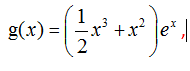- 利用导数求参数的取值范围
- 共134题
12.定义在






正确答案
解析
过构造函数最后通过函数的奇偶性和单调性判断使


考查方向
解题思路
通过构造函数最后通过函数的奇偶性和单调性来解答。
易错点
不知道通过函数的性质以及构造函数来解答。
知识点
16.若对



正确答案
解析
将已经不等式可以化为





考查方向
解题思路
本题考查求参数的取值范围的问题,先将已知的不等式化简变形,然后再来求解参数的取值范围。
易错点
不会将已知的不等式化简变形。
知识点
已知函数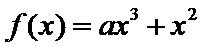
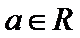
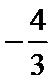
(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分)
22.确定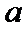
23.若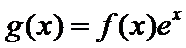
正确答案
解析
试题分析:先求出函数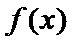
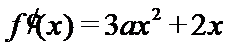
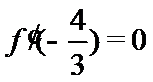
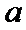
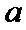
试题解析: (1)对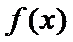
因为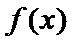
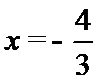
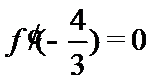
即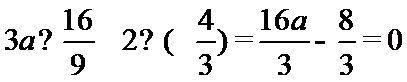
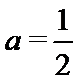
考查方向
解题思路
本题考查函数导数的概念和运算,导数与函数极值之间的关系,利用函数的极值点必是导数为零的点,本题属于中档题.
易错点
极值的几何意义
正确答案
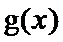
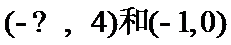
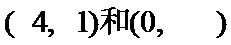
解析
试题分析:由(Ⅰ)的结果可得函数
,利用积的求导法则可求出
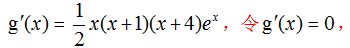
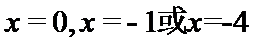
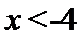
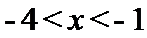
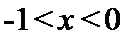
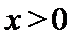
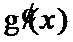
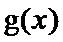
(2)由(1)得,,
故
令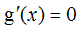
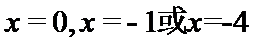
当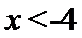
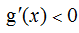
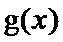
当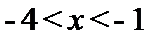
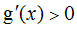
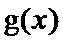
当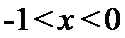
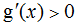
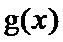
当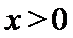
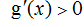
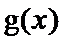
综上知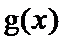
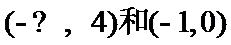
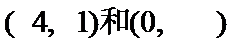
考查方向
解题思路
本题考查函数导数的概念和运算,运用导数研究函数的单调性,使导函数大于零的x的区间函数必增,小于零的区间函数必减进行求解,本题属于中档题.
易错点
注意求导的准确性及使导函数大于零或小于零的x的区间的确定.
21.已知函数f(x)=(x -2)ex+a(x -1)2.
(Ⅰ)讨论f(x)的单调性; (Ⅱ)若有两个零点,求a的取值范围.
正确答案
1
知识点
10.函数


正确答案
解析
依题意, 方程f'(x)=2即
考查方向
导数的几何意义。
解题思路
可转化为方程有解的问题。
易错点
解题时容易忽略定义域。
教师点评
本题难度不大。
知识点
扫码查看完整答案与解析