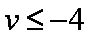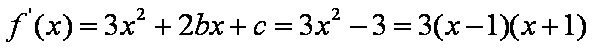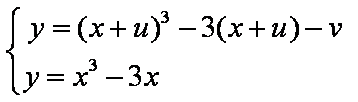- 利用导数求参数的取值范围
- 共134题
角




正确答案
解析
略
知识点
如图,已知C是以AB为直径的元O上一点,
(1)求证:CG是元O的切线
(2)若
正确答案
见解析
解析
解析:
(1)证明:连接CB、OC,
∵CH⊥AB,DB⊥AB,∴CH // BD,
∴
∵AB是直径,∴∠ACB=90°∴∠BCD=90°
在Rt△BCD中
∴∠BCF=∠CBF=90°-∠CBA=∠CAB=∠ACO
∵∠ACB=90°∴∠OCF=90°,∴CG是⊙O的切线.
(2)由FC=FB=FE得:∠FCE=∠FEC,

得:
由切割线定理得:(2+FG)2=BG×AG=2BG2 ……①
在Rt△BGF中,由勾股定理得:BG2=FG2-BF2 ……②
由①、②得:FG2-4FG-12=0,解之得:FG=6或FG=-2(舍去)
∴AB=BG=

知识点
已知函数
(1)若

(2)若


正确答案
见解析
解析
(1)当













(2)由







令




∴
即


知识点
已知函数
(1)若


(2)若

正确答案
(1)
(2)
解析
(1)由


所以

所以所求切线方程为
即
(2)由已知

因为函数

即不等式

令

当


当


由此得


知识点
已知函数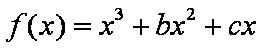
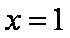
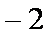
(1)求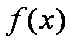
(2)若对任意的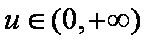
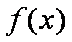
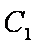

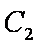
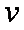
正确答案
(1)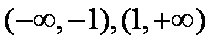
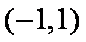
(2)
解析
(1)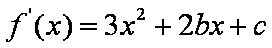
由题意得: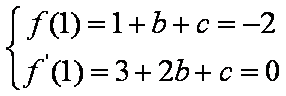
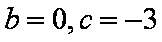
∴
∴当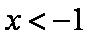
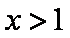

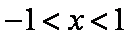
∴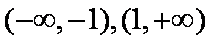
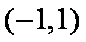
(2)
由方程组
得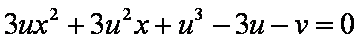
∴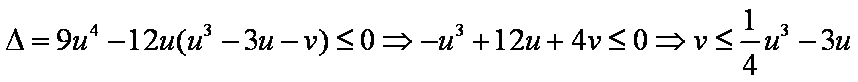
……………………………………9 分
令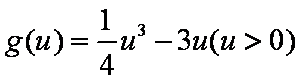
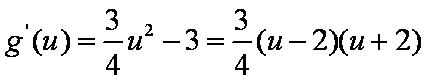
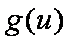
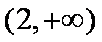
所以当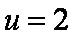
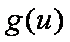
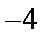
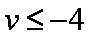
知识点
扫码查看完整答案与解析