- 利用导数求参数的取值范围
- 共134题
已知函数


(1)求

(2)对函数



正确答案
见解析
解析
解析:
(1)由
而点


又直线
故有
(2)由(1)得
由

令
令
故

故当

当
从而当





故
要使



知识点
已知

(1)若


(2)求
(3)设



正确答案
见解析
解析
(1) 


经检验, 
(2) 
(i)当


(ii)当

① 若




② 若



综上所述,当


当



(3)当


易知


注意到
故由题设知

故

知识点
已知函数

(1)若曲线y=f(x)与y=g(x)在x=1处的切线相互平行,求两平行直线间的距离;
(2)若f(x)≤g(x)-1对任意x>0恒成立,求实数a的值;
(3)当a<0时,对于函数h(x)=f(x)-g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为

正确答案
见解析
解析
(1)
曲线y=f(x)在x=1处的切线为2x-y-2=0,
曲线y=g(x)在x=1处的切线方程为2x-y-1=0. ……………3分
两直线间的距离为
(2)令h(x)=f(x)-g(x)+1, ,则
当a≤0时, 注意到x>0, 所以
又h(1)=0,故0<x<1时,h(x)>0,即f(x)> g(x)-1,与题设矛盾. ……………6分
当a>0时,
当


所以h(x)在上是增函数,在上是减函数, ……………8分
∴h(x)≤
因为h(1)=0,又当a≠2时,≠1,

所以a=2. ……………9分
(3)当a<0时,由(2)知
不妨设0<x1≤x2,则|h(x1)-h(x2)|=h(x1)-h(x2),|x1-x2|=x2-x1, ……………10分
∴|h(x1)-h(x2)|≥|x1-x2
等价于h(x1)-h(x2)≥x2-x1,即h(x1)+x1≥h(x2)+x2, ……………11分
令H(x)=h(x)+x=alnx-x2+x+1,H(x)在(0,+∞)上是减函数,
∵
∴-2x2+x+a≤0在x>0时恒成立,∴a≤(2x2-x)min ……………13分
又x>0时, (2x2-x)min=
∴a≤-,又a<0,∴a的取值范围是
知识点
如图,已知点







(1)求

(2)设动点





正确答案
见解析。
解析
(1)由题意可知


在

故椭圆的标准方程为:
(2)设
∵M.N在椭圆上,∴
又直线OM与ON的斜率之积为

于是


知识点
点(x,y)满足
正确答案
解析
实数x,y满足不等式组 
由图可知,当x=a,y=1﹣a时,
目标函数z=x﹣2y取得最大值,
即1=a﹣2×(1﹣a),解得:a=1
故选A。
知识点
如图,








(1) 求证:
(2)求证:
正确答案
见解析。
解析
(1) 由







(2)由






知识点
过点

正确答案
解析
圆的标准方程是:(x+1)2+(y-2)2=132,圆心(-1,2),半径r=13过点
A(11,2)的最短的弦长为10,最长的弦长为26,(分别只有一条)还有长度为11,12,…,25的各2条,所以共有弦长为整数的2+2×15=32条,故选C
知识点
20.已知函数f(x)=
(1)当a=1时,求f(x)的最小值;
(2)若f(x)在(0,e]上的最小值为2,求实数a的值;
(3)当a=﹣1时,试判断函数g(x)=f(x)+
正确答案
(1)1
(2)a=e
(3)见解析。
解析
(1)当a=1时,
当x∈(0,1)时,f′(x)<0,f(x)单调递减,
当x∈(1,+∞)时,f′(x)>0,f(x)单调递增,
所以,当x=1时,f(x)有最小值:f(x)min=f(1)=1.
(2)因为
①当a≤0时,f′(x)>0,f(x)在(0,e]上为增函数,此时f(x)在(0,e]上无最小值.
②当a∈(0,e]时,若x∈(0,a),则f′(x)<0,f(x)单调递减,
若x∈(a,e],则f′(x)>0,f(x)单调递增,
所以f(x)min=f(a)=1+lna=2,∴a=e,符合题意;
③当a>e时,x∈(0,e],
∴f′(x)<0,f(x)单调递减,
所以
∴a=e,不符合题意;
综上所述,a=e时符合题意.
(3)证明:当a=﹣1时,函数

令φ(x)=2+x﹣lnx,(x>0),则
所以x∈(0,1)时,φ′(x)<0,φ(x)单调递减,
当x∈(1,+∞)时,φ′(x)>0,φ(x)单调递增,
所以,φ(x)min=φ(1)=3>0,在定义域内g′(x)>0,g(x)在(0,+∞)单调递增,
又g(1)=﹣1<0,而
因此,函数g(x)在(1,e)上必有零点,又g(x)在(0,+∞)单调递增,
所以函数
知识点
17.已知函数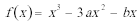
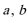
(1)若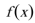
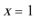
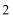
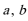
(2)若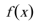
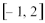
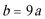
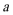
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)求
(2)不等式




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析





















